Bài 71 trang 49 SBT Hình học 10 Nâng cao

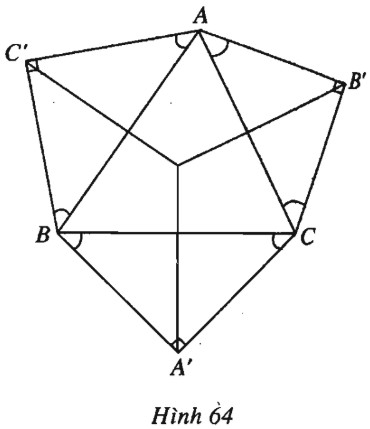
Đề bài

a) Chứng minh rằng nếu \(\alpha \) là góc nhọn thì \(\cos (\alpha  + {90^0}) =  - \sin \alpha \).

b) Cho tam giác nhọn \(ABC\) có các cạnh \(a, b, c\) và diện tích \(S\). Trên ba cạnh và về phía ngoài của tam giác đó dựng các tam giác vuông cân \(A’BC, B’AC, C’AB\) (\(A’, B’, C’\) lần lượt là đỉnh). Chứng minh rằng:

\(A’B’^2+B’C’^2+C’A’^2\) \(=a^2+b^2+c^2+6S.\)

Lời giải chi tiết

(h.64).

a) Ta có

\(\cos \left( {\alpha  + {{90}^0}} \right)\)

\(=  - \cos \left[ {{{180}^0} - (\alpha  + {{90}^0})} \right] \)

\(=  - \cos ({90^0} - \alpha ) =  - \sin \alpha \).

b) Dễ thấy \(AB' = \dfrac{{b\sqrt 2 }}{2} ; \)\( AC' = \dfrac{{c\sqrt 2 }}{2}  ;\) \(  \widehat {B'AC'} = \widehat A + {90^0}\).

Trong tam giác \(AB’C’\) ta có

\(\begin{array}{l}B'C{'^2} = AB{'^2} + AC{'^2} - 2AB'.AC'.\cos \widehat {B'AC'}\\ = \dfrac{{{b^2} + {c^2}}}{2} + bc\sin A\\= \dfrac{{{b^2} + {c^2}}}{2} + 2S.\end{array}\)

Tương tự, \(C'A{'^2} = \dfrac{{{a^2} + {c^2}}}{2} + 2S  ;\) \(  A'B{'^2} = \dfrac{{{a^2} + {b^2}}}{2} + 2S\).

Từ đó suy ra \(A'B{'^2} + B'C{'^2} + C'A{'^2}\) \( = {a^2} + {b^2} + {c^2} + 6S\).

Loigiaihay.com