Bài 72 trang 49 SBT Hình học 10 Nâng cao

Đề bài

Cho từ giác \(ABCD\) nội tiếp được và có các cạnh \(a,b, c, d\). Chứng minh rằng diện tích tứ giác đó được tính theo công thức sau:

\(S = \sqrt {(p - a)(p - b)(p - c)(p - d)} \),trong đó \(p\) là nửa chu vi tứ giác.

Lời giải chi tiết

Giải

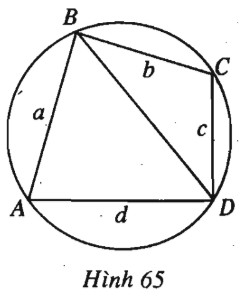
Giả sử \(ABCD\) là tứ giác nội tiếp với độ dài cạnh là \(a, b, c, d\)  (h.65).

Khi đó \(\widehat A + \widehat C = {180^0}\) nên \(\sin C= \sin A ;  \cos C= -\cos A.\)

Ta có

\(S = {S_{ABD}} + {S_{CDB}}\)

\(= \dfrac{1}{2}ad\sin A + \dfrac{1}{2}bc\sin C\)

hay \(2S = (ad + bc)\sin A\), suy ra \(\sin A = \dfrac{{2S}}{{ad + bc}}\).

Mặt khác, tam giác ABD có \(B{D^2} = {a^2} + {d^2} - 2ad\cos A\), còn tam giác CBD có \(B{D^2} = {b^2} + {c^2} - 2bc\cos C\) \( = {b^2} + {c^2} + 2bc\cos A\).

Suy ra \({a^2} + {d^2} - {b^2} - {c^2} = 2(ad + bc)\cos A\) nên \(\cos A = \dfrac{{{a^2} + {d^2} - {b^2} - {c^2}}}{{2(ad + bc)}}\).

Do \({\cos ^2}A + {\sin ^2}A = 1\) nên \(16{S^2} + {({a^2} + {d^2} - {b^2} - {c^2})^2}\) \( = 4{(ad + bc)^2}\).

Vậy \(16{S^2} = {\left[ {2(ad + bc)} \right]^2} - {({a^2} + {d^2} - {b^2} - {c^2})^2}\)

\(\begin{array}{l} = (2ad + 2bc + {a^2} + {d^2} - {b^2} - {c^2})\\(2ad + 2bc - {a^2} - {d^2} + {b^2} + {c^2})\\ = \left[ {{{(a + d)}^2} - {{(b - c)}^2}} \right].\left[ {{{(b + c)}^2} - {{(a - d)}^2}} \right]\\ = (a + d + b - c)(a + d - b + c)\\(b + c + a - d)(b + c - a + d)\\ = (2p - 2c)(2p - 2b)(2p - 2d)(2p - 2a)\\ = 16(p - a)(p - b)(p - c)(p - d).\end{array}\)

Từ đó ta có \(S = \sqrt {(p - a)(p - b)(p - c)(p - d)} \).

Loigiaihay.com