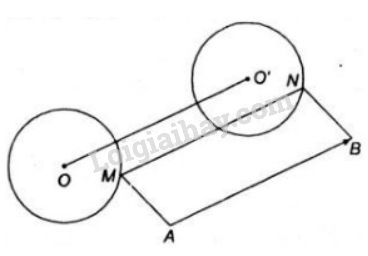
Bài 7 trang 35 SGK Hình học 11Cho hai điểm A,B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Quảng cáo
Đề bài Cho hai điểm \(A,B\) và đường tròn tâm \(O\) không có điểm chung với đường thẳng \(AB\). Qua mỗi điểm \(M\) chạy trên đường tròn \((O)\) dựng hình bình hành \(MABN\). Chứng minh rằng: điểm \(N\) thuộc một đường tròn xác định. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Chứng minh \(N\) là ảnh của \(M\) qua phép tinh tiến theo vecto \((\overrightarrow {AB})\) cố định. +) Xác định ảnh của \(M\) khi \(M\) chạy trên \((O)\). Tức là tìm ảnh của \((O)\) qua phép tịnh tiến. Lời giải chi tiết Vì \(MABN\) là hình bình hành nên \( \overrightarrow {MN}=\overrightarrow {AB}\) không đổi. \( \Rightarrow {T_{\overrightarrow {AB} }}\left( M \right) = N\). Gọi \((O',R)\) là ảnh của \((O,R)\) qua phép tịnh tiến theo \(\overrightarrow {AB}\), cố định. Vì \(M \in (O)\) nên \(N= {T_{\overrightarrow {AB} }}\left( M \right) \in {T_{\overrightarrow {AB} }}\left( (O) \right) = (O')\) Vậy \(N \in (O')\) (đpcm). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
