Bài 69 trang 49 SBT Hình học 10 Nâng caoGiải bài tập Bài 69 trang 49 SBT Hình học 10 Nâng cao Quảng cáo
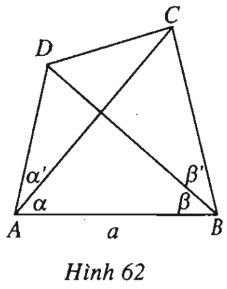
Đề bài Cho tứ giác \(ABCD\) có \(AB = a , \widehat {CAB} = \alpha ,\)\( \widehat {DBA} = \beta , \widehat {DAC} = \alpha ' , \widehat {CBD} = \beta '\). Tính độ dài cạnh \(CD\). Lời giải chi tiết (h.62).
Tính \(AD\) và \(AC\) như bài 68 ta được \(AD = \dfrac{{a\sin \beta }}{{\sin (\alpha + \alpha ' + \beta )}} , \) \( AC = \dfrac{{a\sin (\beta + \beta ')}}{{\sin (\alpha + \beta + \beta ')}}\). Sau đó áp dụng đính lí cosin vào tam giác \(ACD\) ta có \(C{D^2} = A{C^2} + A{D^2} - 2AC.AD.\cos \alpha '\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
