Bài 55 trang 47 SBT Hình học 10 Nâng cao

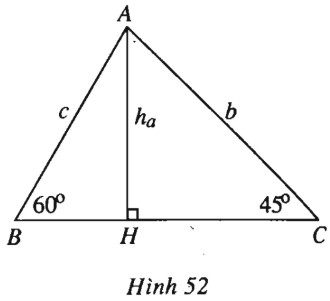
Đề bài

Tam giác \(ABC\) có \(\widehat B = {60^0}; \widehat C = {45^0}; BC = a\).

a) Tính độ dài hai cạnh \(AB, AC.\)

b) Chứng minh \(\cos {75^0} = \dfrac{{\sqrt 6  - \sqrt 2 }}{4}\).

Lời giải chi tiết

a) Ta có \(\widehat A = {180^0} - ({60^0} + {45^0}) = {75^0}.\)

Đặt \(AC=b, AB=c\). Theo định lí hàm sớ sin:

\(\dfrac{b}{{\sin {{60}^o}}} = \dfrac{a}{{\sin {{75}^0}}} = \dfrac{c}{{{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}}\).

Suy ra \(b = \dfrac{{a\sqrt 3 }}{{2\sin {{75}^0}}}  ;   c = \dfrac{{a\sqrt 2 }}{{2\sin {{75}^0}}}.\)

b) Kẻ \(AH \bot BC\) (h.52), do \(\widehat B, \widehat C\) đều là góc nhọn nên \(H\) thuộc đoạn \(BC\), hay \(BC=HB+HC\). Ta có

\(\begin{array}{l}\left\{ \begin{array}{l}HC = \dfrac{{b\sqrt 2 }}{2}\\HB = \dfrac{c}{2}\end{array} \right.\\ \Rightarrow  a = HC + HB = b\dfrac{{\sqrt 2 }}{2} + \dfrac{c}{2} \\= \dfrac{{a\sqrt 6  + a\sqrt 2 }}{{4.\sin {{75}^0}}}   \\ \Rightarrow   \sin {75^0} = \dfrac{{\sqrt 6  + \sqrt 2 }}{4}.\\\cos {75^0} = \sqrt {1 - {{\sin }^2}{{75}^0}}\\  = \sqrt {1 - {{\left( {\dfrac{{\sqrt 6  + \sqrt 2 }}{4}} \right)}^2}} \\ = \dfrac{1}{4}\sqrt {8 - 2\sqrt {12} } \\ = \dfrac{1}{4}\sqrt {{{\left( {\sqrt 6  - \sqrt 2 } \right)}^2}}  = \dfrac{{\sqrt 6  - \sqrt 2 }}{4}\end{array}\)

Loigiaihay.com