Bài 54: Phân số và phép chia số tự nhiên (tiết 2) trang 49 Vở thực hành Toán 4Viết thương của mỗi phép chia sau dưới dạng phân số ... Nối số đo thích hợp với cách đọc số đo đó Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu) a) Mẫu: $21:25 = \frac{{21}}{{25}}$ 30 : 43 = ............... 61 : 69 = .............. 17 : 100 = .............. b) Mẫu: $9:4 = \frac{9}{4}$ 51 : 7 = ............ 60 : 39 = ............. 200 : 163 = ........... Phương pháp giải: Thương của phép chia một số tự nhiên cho một số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia. Lời giải chi tiết:
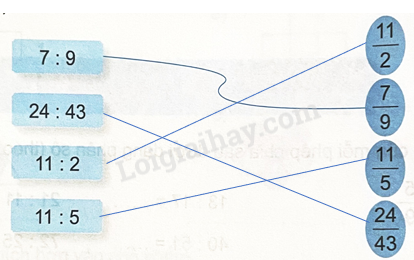
Câu 2 Nối (theo mẫu).
Phương pháp giải: Thương của phép chia một số tự nhiên cho một số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia. Lời giải chi tiết:
Câu 3 Viết số vào chỗ chấm cho thích hợp.
Phương pháp giải: Quan sát hình rồi viết phân số thích hợp vào chỗ chấm. Lời giải chi tiết:
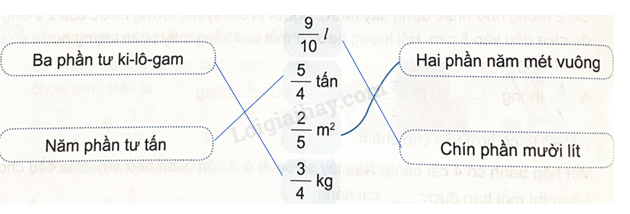
Câu 4 Nối số đo thích hợp với cách đọc số đo đó (theo mẫu).
Phương pháp giải: Chọn số đo thích hợp với cách đọc số đo đó Lời giải chi tiết:
Câu 5 Viết phân số thích hợp vào chỗ chấm (theo mẫu).
Mẫu: AC = $\frac{1}{5}$ AB ; AD = .......... AB ; AE = .......... AB ; AG = .......... AB b) Nếu AB = 1 m thì độ dài các đoạn thẳng AC, AD, AE, AG bằng mấy phần của 1 m? Mẫu: AC = $\frac{1}{5}$ m ; AD = ......... m ; AE = .......... m ; AG = ......... m Phương pháp giải: Quan sát ví dụ mẫu để tìm phân số thích hợp với các đoạn thẳng đã cho. Lời giải chi tiết: a) \({\text{AD}} = \frac{2}{5}{\text{ AB}}\) ; \({\text{AE}} = \frac{3}{5}{\text{AB}}\) ; \({\text{AG}} = \frac{4}{5}{\text{AB}}\) b) \({\text{AD}} = \frac{2}{5}{\text{m}}\) ; \({\text{AE}} = \frac{3}{5}{\text{m\;}}\) ; \({\text{AG}} = \frac{4}{5}{\text{m}}\)
|