Giải bài 5 trang 29 SGK Đại số và Giải tích 11Giải các phương trình sau: Quảng cáo
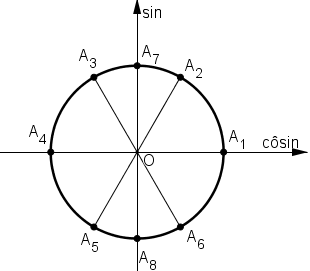
Video hướng dẫn giải Giải các phương trình sau: LG a \(\begin{array}{l}\tan \left( {x - {{15}^0}} \right) = \frac{{\sqrt 3 }}{3}\\\end{array}\) Phương pháp giải: Coi biểu thức sau hàm tan như một ẩn phụ khác, giải tương tự như pt LG cơ bản \(\begin{array}{l} Lời giải chi tiết: Điều kiện \(x - 15^0\neq 90^0+k180^0 \) \(\Leftrightarrow x\neq 105^0+k.180^0.\) \(tan (x - 15^0) = \frac{\sqrt{3}}{3}\) \( \Leftrightarrow tan(x-15^0)=tan30^0\) \(\Leftrightarrow x - 15^0 = 30^0 + k180^0 , (k \in \mathbb{Z}).\) \(\Leftrightarrow x = 45^0 + k180^0 , (k \in \mathbb{Z}).\) (tm) Vậy nghiệm của phương trình là: \(x = 45^0 + k180^0 , (k \in \mathbb{Z}).\) LG b \(\begin{array}{l}\,\,\cot \left( {3x - 1} \right) = - \sqrt 3 \\\end{array}\) Phương pháp giải: Coi biểu thức sau hàm cot như một ẩn phụ lớn, giải tương tự như pt LG cơ bản \(\begin{array}{l}\,\,\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\,\left( {k \in Z} \right)\\\end{array}\) Lời giải chi tiết: Điều kiện \(3x-1\neq k\pi (k\in \mathbb{Z})\) hay \(x\neq \frac{1+k \pi}{3}(k\in \mathbb{Z})\) \(\begin{array}{l} Vậy nghiệm phương trình là \(x=\frac{1}{3}-\frac{\pi }{18}+\frac{k\pi }{3},(k\in \mathbb{Z})\) LG c \(\begin{array}{l}\,\,\cos 2x\tan x = 0\\\end{array}\) Phương pháp giải: \(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l} Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức. Lời giải chi tiết: Điều kiện \(cosx\neq 0\Leftrightarrow x\neq \frac{\pi }{2}+k\pi (k\in \mathbb{Z})\) \(\begin{array}{l} Vậy nghiệm phương trình là: \(x=\frac{\pi }{4}+\frac{k\pi }{2}(k\in \mathbb{Z})\) hoặc \(x=k\pi (k\in \mathbb{Z})\) LG d \(\begin{array}{l}\,\,\sin 3x\cot x = 0 Phương pháp giải: \(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l} Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức. Lời giải chi tiết: ĐK: \(sinx\neq 0\Leftrightarrow x\neq k\pi (k\in \mathbb{Z})\) \(\begin{array}{l} Kết hợp với điều kiện ta thấy khi \(k = 3m,m \in \mathbb{Z}\) thì \(x = \frac{{k\pi }}{3} = \frac{{3m\pi }}{3} = m\pi \,\,\left( {m \in Z} \right)\) \( \Rightarrow \sin x = 0\) không thỏa điều kiện. Vậy phương trình có nghiệm là: \(x=\frac{k \pi}{3}\) \(\,\left( {k \ne 3m\,\,\left( {m \in Z} \right)} \right)\) và \(x=\frac{\pi }{2}+n\pi \,\,(n \in Z)\). Chú ý: Biểu diễn các họ nghiệm trên đường tròn lượng giác để loại nghiệm: Các nghiệm \(\left[ \begin{array}{l}x = \dfrac{{k\pi }}{3}\\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\) được biểu diễn bởi các điểm từ A1 đến A8 trên đường tròn lượng giác như hình dưới.
Với điều kiện x ≠ k.π nên các điểm A1 và A4 bị loại. Vậy họ nghiệm chỉ còn lại các điểm A2; A3; A5; A6; A7; A8 và ta viết được dưới kết quả \(\left[ \begin{array}{l}x = \pm \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\). Loigiaihay.com
|




















Danh sách bình luận