Giải bài 7 trang 29 SGK Đại số và Giải tích 11Giải các phương trình sau: Quảng cáo
Video hướng dẫn giải Giải các phương trình sau: LG a \(\begin{array}{l}\,\,\sin 3x - \cos 5x = 0\\\end{array}\) Phương pháp giải: B1: chuyển vế, đưa PT về dạng \(sin \alpha= cos \beta\). B2: Do \(\sin x = \cos \left( {\frac{\pi }{2} - x} \right)\) PT trở về dạng \(\cos X = \cos Y \) với \(X=\left( {\frac{\pi }{2} - x} \right); Y= \beta\) \(\Leftrightarrow \left[ \begin{array}{l}X =Y + k2\pi \\ X = - Y + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\) Từ đó suy ra nghiệm x và KL. Lời giải chi tiết: \(\begin{array}{l}\,\,\sin 3x - \cos 5x = 0\\\Leftrightarrow \cos 5x=\sin 3x = \cos \left( {\frac{\pi }{2} - 3x} \right)\\\Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} - 3x + k2\pi \\5x = - \frac{\pi }{2} + 3x + k2\pi \end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}8x = \frac{\pi }{2} + k2\pi \\2x = - \frac{\pi }{2} + k2\pi \end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\\x = - \frac{\pi }{4} + k\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)\end{array}\) Vậy nghiệm phương trình là: \(x=\frac{\pi }{16}+\frac{k\pi }{4} (k\in Z)\) và \(x=-\frac{\pi }{4} +k\pi, (k\in \mathbb{Z})\) Cách khác: sin3x - cos5x = 0
Vậy nghiệm phương trình là: \(x=\frac{\pi }{16}+\frac{k\pi }{4} (k\in Z)\) và \(x=-\frac{\pi }{4} +k\pi, (k\in \mathbb{Z})\) LG b \(\begin{array}{l}\,\,\tan 3x\tan x = 1\end{array}\) Phương pháp giải: B1: Tìm ĐKXĐ. B2: vì \(\frac{1}{{\tan x}} = \cot x = \tan \left( {\frac{\pi }{2} - x} \right)\) phương trình trở về dạng \(\tan \alpha = \tan \beta \) với \(\alpha = 3x; \beta =\frac{\pi }{2} - x\) \(\Leftrightarrow \alpha = \beta + k\pi \,\,\left( {k \in Z} \right)\) B3: Suy ra nghiệm x rồi KL. Lời giải chi tiết: Điều kiện: \(\begin{array}{l}\left\{ \begin{array}{l}\cos 3x \ne 0\\\cos x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x \ne \frac{\pi }{2} + k\pi \\x \ne \frac{\pi }{2} + k\pi \end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{6} + \frac{{k\pi }}{3}\\x \ne \frac{\pi }{2} + k\pi \end{array} \right. \Rightarrow x \ne \frac{\pi }{6} + \frac{{k\pi }}{3}\,\,\left( {k \in Z} \right)\end{array}\) \(\begin{array}{l}\tan 3x\tan x = 1\\\Leftrightarrow \tan 3x = \frac{1}{{\tan x}} \\ \Leftrightarrow \tan 3x = \cot x \\ \Leftrightarrow \tan 3x = \tan \left( {\frac{\pi }{2} - x} \right)\\ \Leftrightarrow 3x = \frac{\pi }{2} - x + k\pi \\\Leftrightarrow 4x = \frac{\pi }{2} + k\pi \\\Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\,\left( {k \in Z} \right)\,\,\,\left( {tm} \right)\end{array}\) Vậy nghiệm phương trình là \(x=\frac{\pi }{8}+\frac{k \pi }{4}, \)\(k \in \mathbb{Z}\). Chú ý: Ở bài này ta thấy ngay họ nghiệm \(x=\frac{\pi }{8}+\frac{k \pi }{4}, k \in \mathbb{Z}\) không có nghiệm nào vi phạm điều kiện xác định nên ta lấy cả họ nghiệm và không phải loại bỏ điểm nào. Loigiaihay.com
|














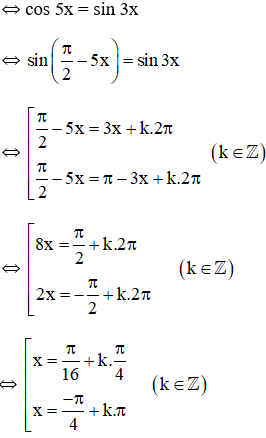






Danh sách bình luận