Bài 44 trang 86 SGK Toán 9 tập 2

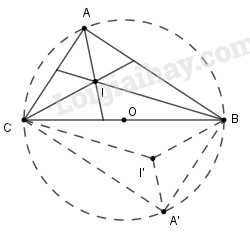
Đề bài

Cho tam giác $ABC$ vuông ở $A$, có cạnh $BC$ cố định. Gọi $I$ là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm $I$ khi $A$ thay đổi.

Lời giải chi tiết

                              

* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.

* Chứng minh :

Phần thuận : 

Điểm A luôn nhìn đoạn thẳng AB dưới một góc $90^\circ$ nên quỹ tích điểm $A$ là đường tròn đường kính $BC.$

Xét tam giác $ABC$ vuông tại $A$ nên $\widehat {ACB} + \widehat {ABC} = 90^\circ$, lại có $BI$ là phân giác góc $B$ và $CI$ là phân giác góc $C$ nên

$\widehat {ICB} = \dfrac{1}{2}\widehat {ACB};\,\widehat {IBC} = \dfrac{1}{2}\widehat {ABC} \Rightarrow \widehat {ICB} + \widehat {IBC} = \dfrac{1}{2}\left( {\widehat {ACB} + \widehat {ABC}} \right) = \dfrac{1}{2}.90^\circ  = 45^\circ$

Xét tam giác $IBC$ có $\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ  \Leftrightarrow \widehat {BIC} = 180^\circ  - 45^\circ  = 135^\circ$

Nên số đo góc $BIC$ luôn không đổi.

Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc $135^\circ .$

Vậy điểm I thuộc hai cung chứa góc $135^\circ$ dựng trên đoạn BC.

Phần đảo: 

Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện. 

+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC

+ Kẻ tia Bx sao cho BI là phân giác của góc CBx

+ Kẻ tia Cy sao cho CI là phân giác của góc BCy

+ Bx cắt Cy tại A.

Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC

Ta có: 

$\begin{array}{l} \widehat {BAC} = {180^0} - \left( {\widehat B + \widehat C} \right)\\ = {180^0} - 2\left( {\widehat {IBC} + \widehat {ICB}} \right)\\ = {180^0} - 2\left( {{{180}^0} - \widehat {BIC}} \right)\\ = {180^0} - {360^0} + {2.135^0}\\ = {90^0} \end{array}$

Vậy ΔABC vuông tại A thỏa mãn đề bài. 

Kết luận: Quĩ tích các điểm I là hai cung chứa góc $135^\circ$ dựng trên đoạn BC.

Loigiaihay.com