Bài 40 trang 23 SGK Toán 9 tập 1

Đề bài

Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

$0,71$;                     $0,03;$                     $0,216;$

$0,811$;                  $0,0012;$                  $0,000315.$

Lời giải chi tiết

Khi dùng bảng số:

Trước hết ta cần chia số trong căn cho 100, 10000 ... 

- Ta có: $\sqrt{0,71} =\sqrt{71} :\sqrt{100} =\sqrt{71}: 10$

Tra bảng: $\sqrt{71} ≈ 8,426$ nên $\sqrt{0,71}≈ 8,426 : 10 = 0,8426$ 

- Tra bảng: $\sqrt{0,03} =\sqrt{3} :\sqrt{100}$$≈ 1,732 : 10 =0,1732$

- Tra bảng: $\sqrt{0,216} =\sqrt{21,6} :\sqrt{100}$$≈ 4,648 : 10 = 0,4648$

- Tra bảng: $\sqrt{0,811} =\sqrt{81,1} :\sqrt{100}$$≈ 9,006 : 10 = 0,9006$

- Tra bảng: $\sqrt{0,0012} =\sqrt{12} :\sqrt{10000}$ $≈ 3,464 : 100 = 0,03464$

- Tra bảng: $\sqrt{0,000315} =\sqrt{3,15} :\sqrt{10000}$ $≈ 1,775 : 100 = 0,01775$

Suy ra,

$\sqrt{0,71}\approx 0,8426$

$\sqrt{0,03}\approx 0,1732$

$\sqrt{0,216}\approx 0,4648$

$\sqrt{0,811}\approx 0,9006$

$\sqrt{0,0012}\approx 0,03464$

$\sqrt{0,000315}\approx 0,01775$

Kết quả khi dùng máy tính bỏ túi:

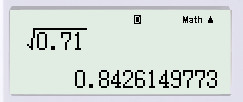
$\sqrt{0,71}\approx 0,842619$

$\sqrt{0,03}\approx 0,173205$

$\sqrt{0,216}\approx 0,46475$

$\sqrt{0,811}\approx 0,90055$

$\sqrt{0,0012}\approx 0,03464$

$\sqrt{0,000315}\approx 0,017748$

Khi dùng máy tính bỏ túi ta được kết quả chính xác hơn và hầu như nhỏ hơn khi dùng bảng số.

Loigiaihay.com