Bài 4 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo

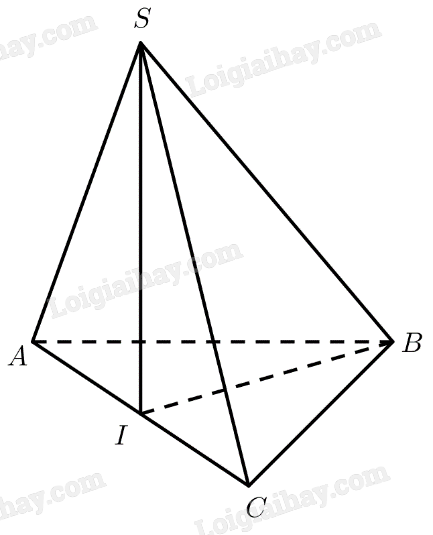
Đề bài

Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {ASB} = 90^\circ ,\widehat {BSC} = {60^ \circ }\) và \(\widehat {ASC} = {120^ \circ }\). Gọi \(I\) là trung điểm cạnh \(AC\). Chứng minh \(SI \bot \left( {ABC} \right)\).

Lời giải chi tiết

 

Xét tam giác \(SAC\) có:

\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}}  = a\sqrt 3 \)

\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)

Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)

\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)

Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}}  = a\sqrt 2 \)

Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy  \(BC = a\)

Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)

\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)

Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)

\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)

Ta có:

\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)