Bài 2 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạoCho hình vuông (ABCD). Gọi (H,K) lần lượt là trung điểm của (AB,AD). Quảng cáo
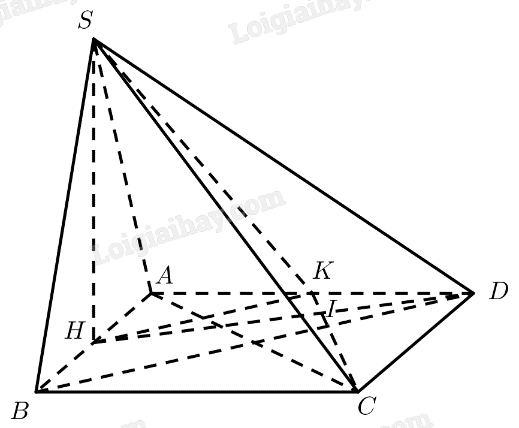
Đề bài Cho hình vuông \(ABCD\). Gọi \(H,K\) lần lượt là trung điểm của \(AB,AD\). Trên đường thẳng vuông góc với \(\left( {ABCD} \right)\) tại \(H\), lấy điểm \(S\). Chứng minh rằng: a) \(AC \bot \left( {SHK} \right)\); b) \(CK \bot \left( {SDH} \right)\). Phương pháp giải - Xem chi tiết Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng. Lời giải chi tiết
a) Ta có: \(H\) là trung điểm của \(AB\) \(K\) là trung điểm của \(AD\) \( \Rightarrow HK\) là đường trung bình của \(\Delta ABD\) \( \Rightarrow HK\parallel B{\rm{D}}\) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\) Ta có: \(\left\{ \begin{array}{l}AC \bot BD\\HK//BD\end{array} \right. \Rightarrow AC \bot HK\) Ta có: \(\left\{ \begin{array}{l}AC \bot HK - cmt\\AC \bot SH\,(Do\,SH \bot (ABCD))\\HK,SH \subset (SHK);HK \cap SH\end{array} \right. \Rightarrow AC \bot (SHK)\) b) Gọi \(I = CK \cap DH\). Xét \(\Delta AH{\rm{D}}\) và \(\Delta DKC\) có: \(\left. \begin{array}{l}AH = DK\\\widehat {HA{\rm{D}}} = \widehat {K{\rm{D}}C}\\A{\rm{D}} = C{\rm{D}}\end{array} \right\} \Rightarrow \Delta AH{\rm{D}} = \Delta DKC\left( {c.g.c} \right) \Rightarrow \widehat {A{\rm{D}}H} = \widehat {DCK}\) Mà \(\widehat {DKC} + \widehat {DCK} = {90^ \circ }\) \(\begin{array}{l} \Rightarrow \widehat {DKC} + \widehat {ADH} = {90^0} \Rightarrow \widehat {DKI} = {180^0} - (\widehat {DKC} + \widehat {ADH}) = {90^0}\\ \Rightarrow DH \bot CK\end{array}\) Ta có: \(\left\{ \begin{array}{l}CK \bot DH - cmt\\CK \bot SH\,\,(Do\,SH \bot (ABCD))\\DH,SH \subset (SDH);DH \cap SH\end{array} \right. \Rightarrow CK \bot (SDH)\)
|




















Danh sách bình luận