Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều

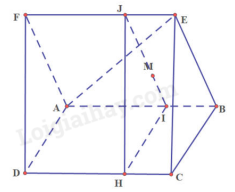
Đề bài

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

a) Chứng minh rằng (AFD) // (BEC).

b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Mặt phẳng (P) cắt đường thẳng AC tại N. Tính \(\frac{{AN}}{{NC}}\).

Lời giải chi tiết

a) Ta có: AD // BC (ABCD là hình bình hành).

Mà AD thuộc (AFD), BC thuộc (BEC).

Suy ra (AFD) // (BEC).

b) Trong (ABEF), kẻ đường thẳng d qua M // AF.

Ta có: d cắt AB tại I, d cắt EF tại J (1)

Trong (ABCD) có I thuộc  (P) mà (P) // (AFD).

Suy ra từ I kẻ IH // AD (2)

Từ (1) và (2) suy ra: (IJH) trùng (P) và // (AFD).

Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD).

Suy ra IH cắt AC tại N.

Ta có các hình bình hành IBCH, IBEJ.

Gọi O là trung điểm của AB.

Ta có M là trọng tâm của tam giác ABE.

Suy ra \(\frac{{MO}}{{ME}} = \frac{1}{2}\).

Ta có AB // CD suy ra AI // CH.

Định lý Ta – let:\(\frac{{AN}}{{NC}} = \frac{{AI}}{{CH}}\).

Mà CH = IB (IBCH là hình bình hành).

Suy ra\(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}}\).

Ta có: AB // EF nên OI // EJ.

Do đó: \(\frac{{OI}}{{{\rm{EJ}}}} = \frac{{MO}}{{ME}} = \frac{1}{2}\).

Mà EJ = IB (IBEJ là hình bình hành).

Suy ra \(\frac{{OI}}{{IB}} = \frac{1}{2}\) hay \(IB = 2OI\).

Ta có \(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}} = \frac{{AO + OI}}{{2OI}}\).

Mà OA = OB (O là trung điểm AB).

Nên \(\frac{{AN}}{{NC}} = \frac{{OB + OI}}{{2OI}} = \frac{{OI + IB + OI}}{{2OI}} = \frac{{OI + 2OI + OI}}{{2OI}} = 2\).

Do đó: \(\frac{{AN}}{{NC}} = 2\).