Bài 36 trang 82 SGK Toán 9 tập 2Cho đường tròn (O) và hai dây AB, AC Quảng cáo
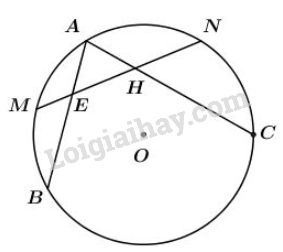
Đề bài Cho đường tròn \((O)\) và hai dây \(AB\), \(AC\). Gọi \(M, N\) lần lượt là điểm chính giữa của cung \(AB\) và cung \(AC\). Đường thẳng \(MN\) cắt dây \(AB\) tại \(E\) và cắt dây \(AC\) tại \(H\). Chứng minh rằng tam giác \(AEH\) là tam giác cân. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Sử dụng: "Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn." Lời giải chi tiết Xét đường tròn (O): Vì \(\widehat {AHM}\) là góc có đỉnh bên trong đường tròn chắn các cung \(AM\) và cung \(NC\) nên \(\widehat {AHM}\)= \(\dfrac{sđ\overparen{AM}+sđ\overparen{NC}}{2}\,\,\, (1)\) Vì \(\widehat {AEN}\) là góc có đỉnh bên trong đường tròn chắn các cung \(AN\) và cung \( MB\) nên \(\widehat {AEN}\)= \(\dfrac{sđ\overparen{MB}+sđ\overparen{AN}}{2}\,\,\, (2)\) Ta có: \(\overparen{AM}=\overparen{MB} (3)\) (\(M\) là điểm chính giữa cung \(AB\)). \(\overparen{NC}=\overparen{AN} (4)\) \(N\) là điểm chính giữa cung \(AC\)). Từ (1),(2), (3), (4), suy ra \(\widehat {AHM}= \widehat {AEN}\). Do đó \(∆AEH\) cân tại A
|




















Danh sách bình luận