Bài 36 trang 11 SBT Hình học 10 Nâng caoGiải bài 36 trang 11 sách bài tập Hình học 10 Nâng cao. Cho tứ giác ABCD. Với số k tùy ý, lấy các điểm M và N sao cho ... Quảng cáo
Đề bài Cho tứ giác \(ABCD\). Với số \(k\) tùy ý, lấy các điểm \(M\) và \(N\) sao cho \(\overrightarrow {AM} = k\overrightarrow {AB} \,;\,\,\overrightarrow {DN} = k\overrightarrow {DC} \). Tìm tập hợp các trung điểm \(I\) của đoạn thẳng \(MN\) khi \(k\) thay đổi. Lời giải chi tiết
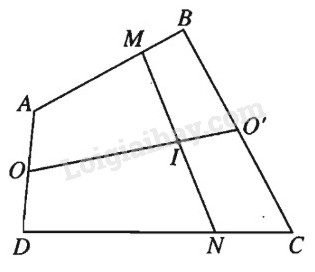
Gọi \(O, O’\) lần lượt là trung điểm của \(AD\) và \(BC\), ta có \(\overrightarrow {OO'} = \dfrac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} ).\) Vì \(O\) và \(I\) là trung điểm của \(AD\) và \(MN\) nên \(\overrightarrow {OI} = \dfrac{1}{2}(\overrightarrow {AM} + \overrightarrow {DN} ) \) \(= \dfrac{k}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\)\( = k\overrightarrow {OO'} \). Do đó O, O', I thẳng hàng. Vậy khi \(k\) thay đổi, tập hợp các điểm \(I\) là đường thẳng \(OO’\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
