Bài 27 trang 9 SBT Hình học 12 Nâng cao

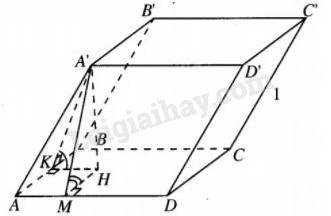
Đề bài

Cho khối hộp \(ABCD.A'B'C'D'\)có đáy là hình chữ nhật với \(AB = \sqrt 3 \), \(AD = \sqrt 7 \). Hai mặt bên \(\left( {ABB'A'} \right)\) và \(\left( {ADD'A'} \right)\) lần lượt tạo với đáy những góc 45⁰ và 60⁰. Hãy tính thể tích khối hộp nếu biết cạnh bên bằng 1.

Lời giải chi tiết

Kẻ \(\eqalign{  & A'H \bot \left( {ABCD} \right)\left( {H \in \left( {ABCD} \right)} \right),  \cr  & HM \bot AD\left( {M \in AD} \right),HK \bot AB\left( {K \in AB} \right). \cr} \)

Theo định lí ba đường vuông góc, ta có

\(AD \bot A'M,AB \bot A'K\)

\( \Rightarrow \widehat {A'MH} = {60^0},\;\widehat {A'KH} = {45^0}\) 

Đặt \(A'H = x\). Khi đó

\(A'H = x;\sin {60^0} = {{2 x } \over\sqrt 3}.\)

\(\eqalign{  & AM = \sqrt {A'{A^2} - A'{M^2}}\cr&  = \sqrt {{{3 - 4{x^2}} \over 3}}  = HK.   \cr} \)

Nhưng \(HK = x\cot {45^0} = x,\)

suy ra \(x = \sqrt {{{3 - 4{x^2}} \over 3}}  \Rightarrow x = \sqrt {{3 \over 7}.} \)

Vậy \({V_{ABCD.A'B'C'D'}} = AD.AB.x \)\(= \sqrt 7 .\sqrt 3 .\sqrt {{3 \over 7}}  = 3.\)

Loigiaihay.com