Bài 24 trang 9 SBT Hình học 12 Nâng caoGiải bài 24 trang 9 sách bài tập Hình học 12 Nâng cao. Đáy của khối lăng trụ đứng... Quảng cáo
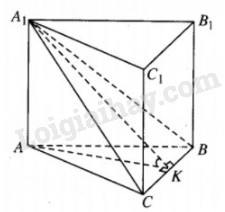
Đề bài Đáy của khối lăng trụ đứng ABC.A1B1C1 là tam giác đều. Mặt phẳng (A1BC) tạo với đáy một góc 300 và tam giác A1BC có diện tích bằng 8. Tính thể tích khối lăng trụ. Lời giải chi tiết
Giả sử CK = x, ở đây AK là đường cao của tam giác đều ABC. Từ định lí ba đường vuông góc, ta có \({A_1}K \bot BC.\) Từ đó góc AKA1 = 300. Xét tam giác vuông A1AK, ta có: \({A_1}K = AK;\cos {30^0} = {{2AK} \over {\sqrt 3 }},\) mà \(AK = {{2x\sqrt 3 } \over 2} = x\sqrt 3 \) nên \({A_1}K = 2x\) \({A_1}A = AK\tan {30^0} = x\sqrt 3 .{{\sqrt 3 } \over 3} = x.\) Vậy \({V_{ABC.{A_1}{B_1}{C_1}}} = CK.AK.{\rm{A}}{{\rm{A}}_1} = {x^3}\sqrt 3 .\) Nhưng \({S_{{A_1}BC}} = CK.{A_1}K = 8\) nên \(x.2x=8 \Rightarrow x = 2\), Vậy \({V_{ABC.{A_1}{B_1}{C_1}}} = 8\sqrt 3 \). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
|
