Bài 21 trang 111 SGK Toán 9 tập 1

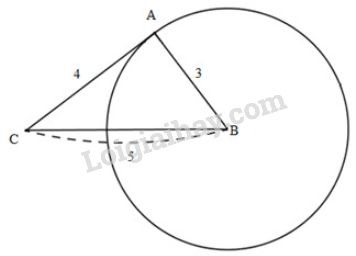
Đề bài

Cho tam giác $ABC$ có $AB=3,\ AC=4,\ BC=5$. Vẽ đường tròn $(B;BA)$. Chứng minh rằng $AC$ là tiếp tuyến của đường tròn. 

Lời giải chi tiết

Xét tam giác $ABC$ ta có:

$BC^2=AB^2+AC^2$ (vì $5^2=3^2+4^2$

Theo định lý Pytago đảo, ta có tam giác $ABC$ vuông tại $A$.

$\Rightarrow$ $AB \bot AC$ tại $A$.

Xét đường tròn (B;BA) có đường thẳng AC đi qua điểm A thuộc đường tròn và AC vuông góc với bán kính BA nên $AC$ là tiếp tuyến của đường tròn.