Bài 20. Một số ví dụ về cách giải các bài toán thuộc phần động lực học trang 80, 81, 82 Vật Lí 10 Kết nối tri thứcNgười ta đẩy một cái thùng có khối lượng 55 kg theo phương ngang với lực 220 N làm thùng chuyển động trên mặt phẳng ngang. Hệ số ma sát trượt giữa thùng và mặt phẳng là 0,35. Tính gia tốc của thùng. Lấy g = 9,8 m/s2 .Một quyển sách đặt trên mặt bàn nghiêng và được thả cho trượt xuống. Cho biết góc nghiêng so với phương ngang. Một học sinh dùng dây kéo một thùng sách nặng 10 kg chuyển động trên mặt sàn nằm ngang. Dây nghiêng một góc chếch lên trên 450 so với phương ngang. Hai vật có khối lượng Quảng cáo
Video hướng dẫn giải Câu hỏi tr 82 B1
Phương pháp giải: Các bước giải bài toán phần động lực học: + Bước 1: Phân tích lực tác dụng lên vật + Bước 2: Chọn hệ quy chiếu + Bước 3: Viết phương trình theo định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \) + Bước 4: Chiếu phương trình định luật 2 Newton lên trục Ox và Oy => Đại lượng cần tính Lời giải chi tiết:
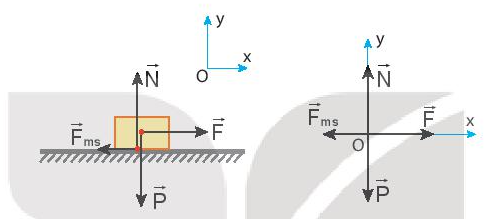
Vật chịu tác dụng của 4 lực: lực đẩy \(\overrightarrow F \), lực ma sát \(\overrightarrow {{F_{ms}}} \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \) Chọn hệ quy chiếu và các lực có chiều như hình vẽ Theo định luật 2 Newton, ta có: \(\overrightarrow F + \overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (1) Chiếu (1) lên trục Ox ta có: \(F - {F_{ms}} = ma \Leftrightarrow F - \mu N = ma\) (2) Chiếu (1) lên Oy, ta có: \(\begin{array}{l}P - N = 0\\ \Leftrightarrow N = P = mg\end{array}\) Thay N = mg vào (2), ta có: \(\begin{array}{l}F - \mu mg = ma\\ \Leftrightarrow a = \frac{{F - \mu mg}}{m}\\ \Leftrightarrow a = \frac{{220 - 0,35.55.9,8}}{{55}} = 0,57(m/{s^2})\end{array}\) Câu hỏi tr 82 B2
Phương pháp giải: Các bước giải bài toán phần động lực học: + Bước 1: Phân tích lực tác dụng lên vật + Bước 2: Chọn hệ quy chiếu + Bước 3: Viết phương trình theo định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \) + Bước 4: Chiếu phương trình định luật 2 Newton lên trục Ox và Oy => Đại lượng cần tính Lời giải chi tiết:
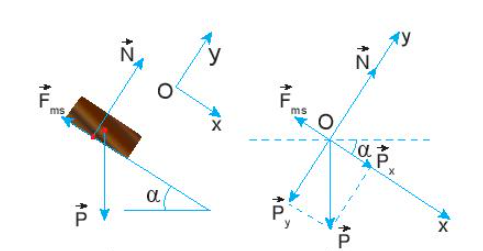
Quyển sách (coi là chất điểm) chịu tác dụng của ba lực: lực ma sát \(\overrightarrow {{F_{ms}}} \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \) Theo định luật 2 Newton, ta có: \(\overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (1) Chiếu (1) lên Ox, ta có: \({P_x} - {F_{ms}} = ma\) \( \Leftrightarrow mg\sin \alpha - \mu N = ma\) (2) Chiếu (1) lên Oy, ta có: \(\begin{array}{l}N - {P_y} = 0\\ \Leftrightarrow N - mg\cos \alpha = 0\\ \Leftrightarrow N = mg\cos \alpha \end{array}\) Thay \(N = mg\cos \alpha \) vào (2), ta có: \(\begin{array}{l}mg\sin \alpha - \mu mg\cos \alpha = ma\\ \Leftrightarrow g\sin \alpha - \mu g\cos \alpha = a\\ \Leftrightarrow a = 9,8.\sin {30^ \circ } - 0,3.9,8.\cos {30^ \circ }\\ \Leftrightarrow a \approx 2,35(m/{s^2})\end{array}\) Quãng đường vật đi được sau 2 s là: \(S = \frac{1}{2}a{t^2} = \frac{1}{2}.2,{35.2^2} = 4,7(m)\) Câu hỏi tr 82 B3
Phương pháp giải: Các bước giải bài toán phần động lực học: + Bước 1: Phân tích lực tác dụng lên vật + Bước 2: Chọn hệ quy chiếu + Bước 3: Viết phương trình theo định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \) + Bước 4: Chiếu phương trình định luật 2 Newton lên trục Ox và Oy => Đại lượng cần tính Lời giải chi tiết:
Chọn hệ quy chiếu như hình vẽ Theo định luật 2 Newton, ta có: \(\overrightarrow F + \overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (1) Chiếu (1) lên Ox, ta có: \({F_x} - {F_{ms}} = ma\) \( \Leftrightarrow F.\cos \alpha - \mu N = ma\) Do vật chuyển động thẳng đều nên a = 0 \( \Rightarrow F.\cos \alpha - \mu N = 0\) (2) Chiếu (1) lên Oy, ta có: \(\begin{array}{l}{F_y} + N - P = 0\\ \Leftrightarrow N = P - {F_y}\\ \Leftrightarrow N = P - F.\sin \alpha \\ \Leftrightarrow N = mg - F.\sin \alpha \end{array}\) Thay \(N = mg - F.\sin \alpha \)vào (2), ta có: \(\begin{array}{l}F.\cos \alpha - \mu (mg - F.\sin \alpha ) = 0\\ \Leftrightarrow F.\cos \alpha - \mu mg + F.\mu .\sin \alpha = 0\\ \Leftrightarrow F(\cos \alpha + \mu .\sin \alpha ) = \mu mg\\ \Leftrightarrow F = \frac{{\mu mg}}{{\cos \alpha + \mu .\sin \alpha }}\\ \Leftrightarrow F = \frac{{0,2.10.9,8}}{{\cos {{30}^0} + 0,2.\sin {{30}^0}}}\\ \Leftrightarrow F \approx 20,29(N)\end{array}\) Câu hỏi tr 82 B4
Phương pháp giải: Các bước giải bài toán phần động lực học: + Bước 1: Phân tích lực tác dụng lên vật + Bước 2: Chọn hệ quy chiếu + Bước 3: Viết phương trình theo định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \) + Bước 4: Chiếu phương trình định luật 2 Newton lên trục Ox và Oy => Đại lượng cần tính Lời giải chi tiết:
Chọn hệ quy chiếu như hình vẽ: Theo định luật 2 Newton cho hệ vật, ta có: \(\overrightarrow {{P_1}} + \overrightarrow {{P_2}} + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{F_{ms2}}} + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = ({m_1} + {m_2}).\overrightarrow a \) (1) Chiếu (1) lên Ox, ta có \(\begin{array}{l}F - {F_{ms1}} - {F_{ms2}} - {T_1} + {T_2} = ({m_1} + {m_2}).a\\ \Leftrightarrow F - \mu ({N_1} + {N_2}) = ({m_1} + {m_2}).a\end{array}\) \( \Leftrightarrow a = \frac{{F - \mu ({N_1} + {N_2})}}{{{m_1} + {m_2}}}\) (2) (do \({T_1} = {T_2}\)) Chiếu (1) lên Oy, ta có: \(\begin{array}{l}{N_1} + {N_2} - {P_1} - {P_2} = 0\\ \Leftrightarrow {N_1} + {N_2} = {P_1} + {P_2}\\ \Leftrightarrow {N_1} + {N_2} = ({m_1} + {m_2}).g\end{array}\) Thay \({N_1} + {N_2} = ({m_1} + {m_2}).g\) vào (2), ta có: \(\begin{array}{l}a = \frac{{F - \mu .g({m_1} + {m_2})}}{{{m_1} + {m_2}}}\\ \Leftrightarrow a = \frac{{45 - 0,2.9,8.(5 + 10)}}{{5 + 10}}\\ \Leftrightarrow a = 1,04(m/{s^2})\end{array}\) Xét vật 1 Theo định luật 2 Newton, ta có \(\overrightarrow {{P_1}} + \overrightarrow {{N_1}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{T_1}} = {m_1}.\overrightarrow a \) (3) Chiếu (3) lên Ox, có \(\begin{array}{l}F - {F_{ms1}} - {T_1} = {m_1}.a\\ \Leftrightarrow {T_1} = F - \mu {N_1} - {m_1}.a\end{array}\) Chiếu (3) lên Oy, ta có \({N_1} = {P_1} = {m_1}.g\) \(\begin{array}{l} \Rightarrow {T_1} = F - \mu {m_1}g - {m_1}.a\\ \Leftrightarrow {T_1} = 45 - 0,2.5.9,8 - 5.1,04\\ \Leftrightarrow {T_1} = 30(N)\end{array}\) Vậy gia tốc của hai vật là 1,04 m/s2 và lực căng của dây nối là 30 N.
|














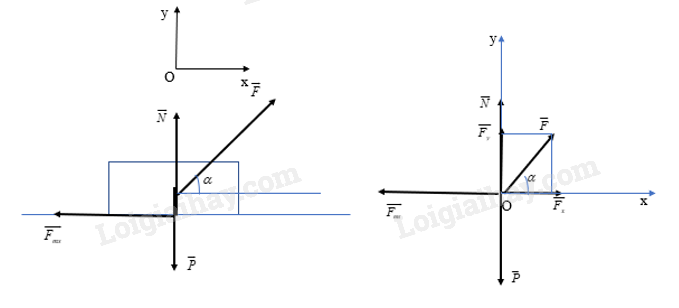 Thùng sách (được coi là chất điểm) chịu tác dụng bởi 4 lực: lực ma sát \(\overrightarrow {{F_{ms}}} \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \), lực kéo \(\overrightarrow F \)
Thùng sách (được coi là chất điểm) chịu tác dụng bởi 4 lực: lực ma sát \(\overrightarrow {{F_{ms}}} \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \), lực kéo \(\overrightarrow F \)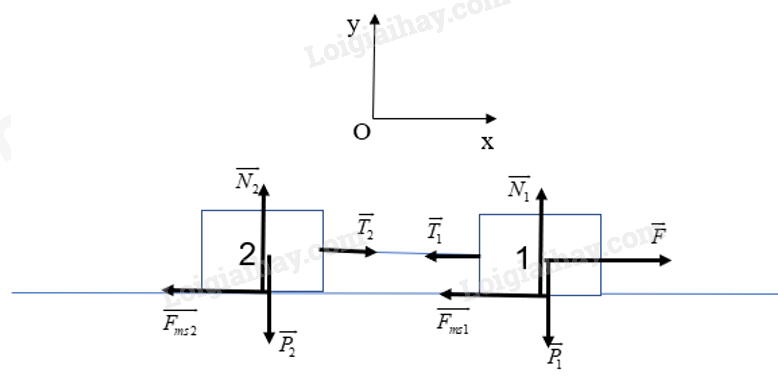






Danh sách bình luận