Bài 12. Chuyển động ném trang 49, 50, 51, 52, 53, 54 Vật Lí 10 Kết nối tri thứcHai viên bi có chạm đất một lúc không. Hãy nhận xét về sự thay đổi vị trí theo phương thẳng đứng của hai viên bi sau những khoảng thời gian bằng nhau. Hãy quan sát ảnh chụp hoạt nghiệm ở Hình 12.2 để chứng tỏ chuyển động thành phần theo phương nằm ngang là chuyển động thẳng đều với vận tốc. Hãy đè xuất phương án thí nghiệm để kiểm tra những kết luận 2 và 3. . Dùng thước kẻ giữ ba viên bi (sắt, thủy tinh và gỗ) trên một tấm thủy tinh đặt nghiêng. Nếu đồng thời ném hai quả bóng giống nhau với nhữn Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Quảng cáo
Video hướng dẫn giải Câu hỏi tr 49 CH 1
Phương pháp giải: Quan sát thí nghiệm và đưa ra dự đoán. Lời giải chi tiết:
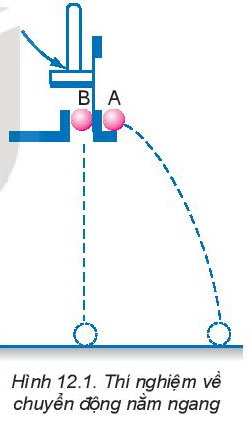
Thông qua thí nghiệm, ta thấy quãng đường viên bi A chuyển động dài hơn quãng đường của viên bi B nên hai viên bi không rơi xuống cùng một lúc, viên bi B sẽ rơi xuống trước viên bi A. Câu hỏi tr 49 CH 2
Phương pháp giải: Quan sát ảnh chụp trong sách giáo khoa Vật lí 10 và đưa ra nhận xét. Lời giải chi tiết:
Qua ảnh chụp hoạt nghiệm chuyển động của hai viên bi A và B, ta thấy rằng sau những khoảng thời gian bằng nhau, tọa độ theo phương Oy của hai viên bi không thay đổi, nhưng tọa độ theo phương Ox của viên bi B thay đổi (lớn dần lên), của viên A trong suốt quá trình chuyển động không thay đổi. Câu hỏi tr 50
Phương pháp giải: Quan sát hình vẽ. Lời giải chi tiết: Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian Mặt khác, ta có \(v = \frac{s}{t} = \frac{x}{t}\) (do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi => vx = v0 Câu hỏi tr 51 HĐ 1
Phương pháp giải: Tự thực hiện thí nghiệm Lời giải chi tiết: 1. Kết luận 1 và 2 là: + Nếu từ cùng một độ cao đồng thời ném các vật khác nhau với vận tốc khác nhau thì vật nào có vận tốc ném lớn hơn sẽ có tầm xa lớn hơn + Nếu từ các độ cao khác nhau ném ngang các vật với cùng vận tốc thì vật nào được ném ở độ cao lớn hơn sẽ có tầm xa lớn hơn Phương án thí nghiệm: Lấy một viên bi và một quả bóng, cùng ném từ một độ cao, ném viên bi với vận tốc lớn hơn khi ném quả bóng, sau khi ném xong hai vật thì ta đo khoảng cách từ chỗ ta đang đứng đến vật. 2. Tầm xa của ba viên bi là như nhau Học sinh tự làm thí nghiệm kiểm tra Câu hỏi tr 51 CH 1
Phương pháp giải: Thời gian rơi của vật: \(t = \sqrt {\frac{{2h}}{g}} \) Biểu thức tính tầm xa: \(L = {v_0}.t = {v_0}\sqrt {\frac{{2h}}{g}} \) Vận tốc của vật khi chạm đất: \({v^2} = v_0^2 + 2gh\) Lời giải chi tiết: 1. a) Từ biểu thức tính thời gian rơi của vật \(t = \sqrt {\frac{{2h}}{g}} \), ta có t2 tỉ lệ thuận với h, mà h1 < h2 => \({t_1} < {t_2}\) => Quả bóng ném ở độ cao h1 chạm đất trước b) Từ biểu thức tính tầm xa \(L = {v_0}.t = {v_0}\sqrt {\frac{{2h}}{g}} \), vận tốc ban đầu của hai quả bóng như nhau, \({t_1} < {t_2}\) => \({L_1} < {L_2}\) => Quả bóng ném ở độ cao h2 có tầm xa lớn hơn 2. a) Thời gian gói hàng chạm đất là: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.490}}{{9,8}}} = 10(s)\) b) Tầm xa của gói hàng là: \(L = {v_0}.t = 100.10 = 1000(m)\) c) Vận tốc của gói hàng khi chạm đất là: \(\begin{array}{l}{v^2} = v_0^2 + 2gh\\ \Rightarrow v = \sqrt {v_0^2 + 2gh} = \sqrt {{{100}^2} + 2.9,8.490} \approx 140(m/s)\end{array}\) Câu hỏi tr 51 CH 2
Phương pháp giải: Liên hệ thực tế. Lời giải chi tiết: Ví dụ về chuyển động ném xiên trong đời sống: + Ném bóng rổ + Ném bóng khi học thể dục môn bóng ném + Đánh bóng tennis... Câu hỏi tr 53 Người ta bắn một viên bi với vận tốc ban đầu 4 m/s theo phương xiên 450 so với phương nằm ngang. Coi sức cản của không khí là không đáng kể.
Phương pháp giải: 1. + Vận tốc ban đầu của vật tính theo phương ngang: \({v_{0x}} = {v_0}.\cos \alpha \) + Vận tốc ban đầu của vật tính theo phương thẳng đứng: \({v_{0y}} = {v_0}.\sin \alpha \) + Vận tốc theo phương ngang không thay đổi + Vận tốc của vật theo phương thẳng đứng sau thời gian t: \({v_y} = {v_{0y}} - gt\) 2. + Biểu thức tính tầm cao H: \(H = \frac{{v_{0y}^2}}{{2.g}}\) + Thời gian vật đạt tầm cao H: \(t = \frac{{{v_{0y}}}}{g}\) + Gia tốc của viên bi ở tầm cao H: a = g 3. Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao H 4. + Thời gian vật rơi xuống đất: \(t = \frac{{2.{v_{0y}}}}{g}\) + Vận tốc của viên bi khi chạm sàn: \(v_y^2 = v_{0y}^2 + 2gh\) + Tầm xa L: \(L = \frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\) Lời giải chi tiết: 1. + Vận tốc ban đầu của viên bi theo phương ngang: \({v_{0x}} = {v_0}.\cos \alpha = 4.\cos {45^0} = 2\sqrt 2 (m/s)\) + Vận tốc ban đầu của viên bi theo phương thẳng đứng: \({v_{0y}} = {v_0}.\sin \alpha = 4.\sin {45^0} = 2\sqrt 2 (m/s)\) + Vận tốc của viên bi theo phương ngang sau 0,1 s và sau 0, 2 s là \({v_{0x}} = 2\sqrt 2 m/s\) + Vận tốc của viên bi theo phương thẳng đứng sau 0,1 s là: \({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8.0,1 \approx 1,85(m/s)\) + Vận tốc của viên bi theo phương thẳng đứng sau 0,2 s là: \({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8.0,2 \approx 0,87(m/s)\) 2. a) Thời gian viên bi đạt tầm cao H: \(t = \frac{{{v_{0y}}}}{g} = \frac{{2\sqrt 2 }}{{9,8}} \approx 0,29(s)\) b) Tầm cao H là: \(H = \frac{{v_{0y}^2}}{{2.g}} = \frac{{{{(2\sqrt 2 )}^2}}}{{2.9,8}} \approx 0,4(m)\) c) Gia tốc của viên bi ở tầm cao H là: a = g = 9,8 (m/s2 ) 3. a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao H = 0,4 m b) Viên vi có vận tốc cực tiểu vào thời gian: t = 0,29 s 4. a) Thời gian viên bi chạm mặt sàn là: \(t = \frac{{2.{v_{0y}}}}{g} = \frac{{2.2\sqrt 2 }}{{9,8}} \approx 0,58(s)\) b) Vận tốc của viên bi khi chạm đất là: \(\begin{array}{l}v_y^2 = v_{0y}^2 + 2gh\\ \Rightarrow {v_y} = \sqrt {v_{0y}^2 + 2gh} = \sqrt {{{(2\sqrt 2 )}^2} + 2.9,8.0,4} \approx 4(m/s)\end{array}\) c) Tầm xa của viên bi là: \(L = \frac{{v_0^2.{{\sin }^2}2\alpha }}{g} = \frac{{{{(2\sqrt 2 )}^2}.{{\sin }^2}{{90}^0}}}{{9,8}} \approx 0,82(m)\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
