Bài 2 trang 99 SGK Toán 11 tập 2 - Cánh Diều

Đề bài

Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Lời giải chi tiết

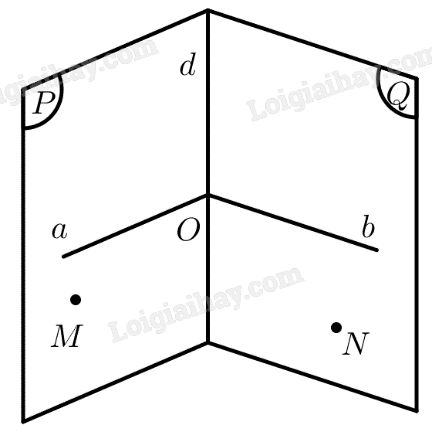
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) vuông góc với nhau. Ta cần chứng minh tồn tại một đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( Q \right)\).

Gọi \(d = \left( P \right) \cap \left( Q \right)\). Lấy \(M \in \left( P \right),N \in \left( Q \right)\) sao cho \(M,N \notin d\).

Gọi góc \(\widehat {aOb}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,d,N} \right]\).

Vì \(\left( P \right) \bot \left( Q \right)\) nên góc nhị diện đó là góc nhị diện vuông. Vậy \(\widehat {aOb} = {90^ \circ } \Rightarrow a \bot b\).

Mà \(a \bot d\)

\( \Rightarrow a \bot \left( Q \right)\)