Bài 2 trang 119 SGK Hình học 11

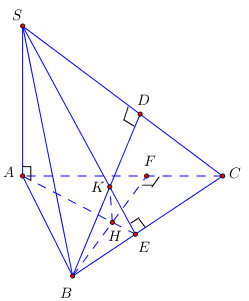
Đề bài

Cho tứ diện \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \((ABC)\). Gọi \(H, K\) lần lượt là trực tâm của tam giác \(ABC\) và \(SBC\).

a) Chứng minh ba đường thẳng \(AH, SK, BC\) đồng quy.

b) Chứng minh rằng \(SC\) vuông góc với mặt phẳng \((BHK)\) và \(HK\) vuông góc với mặt phẳng \((SBC)\).

c) Xác định đường vuông góc chung của \(BC\) và \(SA\).

Lời giải chi tiết

a) Trong \((ABC)\), gọi \(E = AH ∩ BC\).

\(H\) là trực tâm của tam giác \(ABC\) nên \(AE\bot BC\)   (1)

\(SA\bot (ABC)\Rightarrow SA\bot BC\)                             (2)

Từ (1) và (2) suy ra \(BC ⊥ (SAE)\)\( \Rightarrow BC ⊥ SE\).

\(K\) là trực tâm của tam giác \(SBC\Rightarrow SE \) đi qua \(K\) \(\Rightarrow AH, BC, SK\) đồng quy tại \(E\).

b) Trong \((ABC)\) gọi \(F = BH ∩ AC\), trong \((SBC)\) gọi \(D = BK ∩ SC\). Khi đó \((BHK) \equiv (BDF)\).

Ta có:

\(\left\{ \begin{array}{l}
BF \bot AC\\
BF \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)
\end{array} \right.  \Rightarrow BF \bot \left( {SAC} \right)\\ \Rightarrow BF \bot SC\)

\(\left\{ \begin{array}{l}
SC \bot BF\\
SC \bot BD
\end{array} \right. \Rightarrow SC \bot \left( {BDF} \right) \Rightarrow SC \bot \left( {BHK} \right)\)

Ta có: 

\(\begin{array}{l}
SC \bot \left( {BHK} \right) \Rightarrow SC \bot HK\\
BC \bot \left( {SAE} \right) \Rightarrow BC \bot HK\\
\Rightarrow HK \bot \left( {SBC} \right)
\end{array}\)

Cách khác:

Có thể chứng minh \(HK \bot \left( {SBC} \right)\) như sau:

\(\begin{array}{l}
\left\{ \begin{array}{l}
SC \bot \left( {BHK} \right)\\
SC \subset \left( {SBC} \right)
\end{array} \right. \Rightarrow \left( {SBC} \right) \bot \left( {BHK} \right)\\
\left\{ \begin{array}{l}
BC \bot \left( {SAE} \right)\\
BC \subset \left( {SBC} \right)
\end{array} \right. \Rightarrow \left( {SBC} \right) \bot \left( {SAE} \right)\\
\left\{ \begin{array}{l}
\left( {SBC} \right) \bot \left( {BHK} \right)\\
\left( {SBC} \right) \bot \left( {SAE} \right)\\
\left( {BHK} \right) \cap \left( {SAE} \right) = HK
\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right)
\end{array}\)

c) \(\left\{ \begin{array}{l}AE \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\\AE \bot BC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow AE \) là đường vuông góc chung của \(BC\) và \(SA\).

Loigiaihay.com