Bài 13 trang 77 SGK Toán 9 tập 1

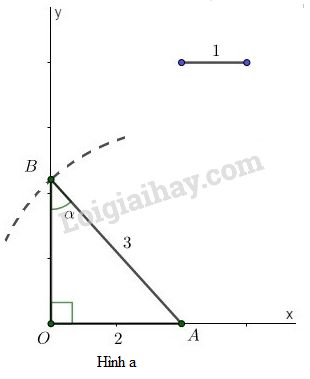
LG a

\(\sin\alpha =\dfrac{2}{3}\)

Phương pháp giải:

+) Dựng một tam giác vuông có hai cạnh là \(m\) và \(n\) (trong đó \(m,\ n\) là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)

+) Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc \(\alpha\).

Lời giải chi tiết:

Ta thực hiện các bước sau:

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) bất kỳ sao cho: \(OA=2\).

- Dùng compa dựng cung tròn tâm \(A\), bán kính \(3\). Cung tròn này cắt \(Oy\) tại điểm \(B\).

- Nối \(A\) với \(B\). Góc \(OBA\) là góc cần dựng.

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\),  theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\sin \alpha = \sin \widehat{OBA} = \dfrac{OA}{AB}=\dfrac{2}{3}\).

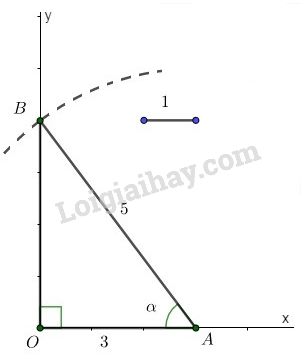
LG b

\(\cos\alpha =0,6\)

Phương pháp giải:

+) Dựng một tam giác vuông có hai cạnh là \(m\) và \(n\) (trong đó \(m,\ n\) là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)

+) Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc \(\alpha\).

Lời giải chi tiết:

Ta có:   \(\cos \alpha =0,6 = \dfrac{3}{5}\)

 - Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) bất kỳ sao cho \(OA=3\).

- Dùng compa dựng cung tròn tâm \(A\) bán kính \(5\). Cung tròn này cắt tia \(Oy\) tại \(B\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}=\alpha \) là góc cần dựng.

Thật vậy, Xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

           \(\cos \alpha =\cos \widehat{OAB}=\dfrac{OA}{AB}=\dfrac{3}{5}=0,6\).

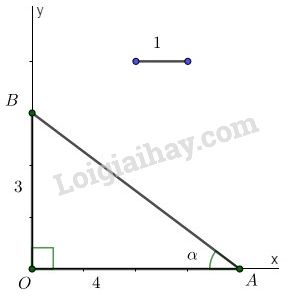
LG c

\(\tan \alpha =\dfrac{3}{4}\)

Phương pháp giải:

+) Dựng một tam giác vuông có hai cạnh là \(m\) và \(n\) (trong đó \(m,\ n\) là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)

+) Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc \(\alpha\).

Lời giải chi tiết:

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA=4\).

   Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB=3\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}\) là góc cần dựng. 

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\tan \alpha =\tan \widehat{OAB}=\dfrac{OB}{OA}=\dfrac{3}{4}.\)

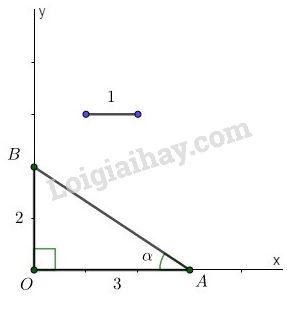
LG d

\(\cot \alpha =\dfrac{3}{2}\) 

Phương pháp giải:

+) Dựng một tam giác vuông có hai cạnh là \(m\) và \(n\) (trong đó \(m,\ n\) là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)

+) Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc \(\alpha\).

Lời giải chi tiết:

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA=3\). 

   Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB=2\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}\) là góc cần dựng.

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\cot \alpha =\cot \widehat{OAB}=\dfrac{OA}{OB}=\dfrac{3}{2}.\)

Loigiaihay.com