Bài 13 trang 106 SGK Toán 9 tập 1

Đề bài

Cho đường tròn $(O)$ có các dây $AB$ và $CD$ bằng nhau, các tia $AB$ và $CD$ cắt nhau tại điểm $E$ nằm bên ngoài đường tròn. Gọi $H$ và $K$ theo thứ tự là trung điểm của $AB$ và $CD$. Chứng minh rằng:

a) $EH = EK$

b) $EA = EC$. 

Lời giải chi tiết

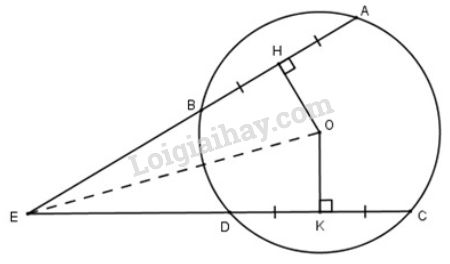
a) Nối OE. 

Vì $HA=HB$  nên  $OH\perp AB$ (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Vì $KC=KD$  nên  $OK\perp CD$. (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Mà $AB=CD$ nên $OH=OK$ (hai dây bằng nhau thì cách đều tâm).

Xét $\Delta HOE$ và $\Delta KOE$ có:

$OH=OK$ 

$EO$ chung

$\widehat{EHO}=\widehat{EKO}=90^0$

$\Rightarrow$ $\Delta HOE=\Delta KOE$ (cạnh huyền - cạnh góc vuông)

$\Rightarrow$ $EH=EK (1)$ ( 2 cạnh tương ứng)

b) Vì $AB=CD$ nên $\dfrac{AB}{2}=\dfrac{CD}{2}$ hay $AH=KC$  (2)

Từ (1) và (2) $\Rightarrow$ $EH+HA=EK+KC$  

hay  $EA=EC.$