Trắc nghiệm Bài 3: Năng lượng trong dao động điều hòa - Vật lí 11 Chân trời sáng tạoĐề bài
Câu 1 :
Một vật nhỏ thực hiện dao động điều hòa theo phương trình x = 5sin(2πt + π/2) (cm;s). Thế năng của vật đó biến thiên với tần số
Câu 2 :
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng 100N/m. khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4cm theo chiều âm thì thế năng của con lắc là
Câu 3 :
Động năng trong dao động điều hoà biển đổi theo thời gian
Câu 4 :
Một vật nhỏ dao động điều hòa dọc theo trục Ox. Khi vật cách vị trí cân bằng một đoạn 2 cm thì động năng của vật là 0,48 J. Khi vật cách vị trí cân bằng một đoạn 6 cm thì động năng của vật là 0,32 J. Biên độ dao động của vật bằng
Câu 5 :
Một vật dao động điều hoà với chu kỳ T, động năng của vật biến đổi theo thời gian
Câu 6 :
Trong dao động điều hòa của một vật thì tập hợp ba đại lượng nào sau đây là không thay đổi theo thời gian
Câu 7 :
Một vật có khối lượng m dao động điều hòa với biên độ A. Khi chu kì tăng 3 lần thì năng lượng của vật sẽ
Câu 8 :
Một chất điểm dao động điều hòa không ma sát. Khi vừa ra khỏi vị trí cân bằng một đoạn S, động năng của chất điểm là 1,8 J. Đi tiếp một đoạn S nữa thì động năng chỉ còn 1,5 J và nếu đi thêm một đoạn S nữa thì động năng bây giờ là? Biết rằng vật chưa đổi chiều chuyển động.
Câu 9 :
Trong dao động điều hòa, ở vị trí nào thì động năng của con lắc có giá trị gấp n lần thế năng?
Câu 10 :
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hoà là sai?
Câu 11 :
Hai con lắc lò xo giống hệt nhau đặt trên cùng mặt phẳng nằm ngang. Con lắc thứ nhất và con lắc thứ hai dao động điều hòa cùng pha với biên độ lần lượt là 3A và A. Chọn mốc thế năng của mỗi con lắc tại vị trí cân bằng của nó. Khi động năng của con lắc thứ nhất là 0,72 J thì thế năng của con lắc thứ hai là 0,24 J. Khi thế năng của con lắc thứ nhất là 0,09 J thì động năng của con lắc thứ hai là
Lời giải và đáp án
Câu 1 :
Một vật nhỏ thực hiện dao động điều hòa theo phương trình x = 5sin(2πt + π/2) (cm;s). Thế năng của vật đó biến thiên với tần số
Đáp án : D Lời giải chi tiết :
Tần số dao động của vật \(f = \frac{\omega }{{2\pi }} = \frac{{2\pi }}{{2\pi }} = 1Hz \Rightarrow {f_{{W_t}}} = 2f = 2Hz\) Đáp án: D
Câu 2 :
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng 100N/m. khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4cm theo chiều âm thì thế năng của con lắc là
Đáp án : B Lời giải chi tiết :
Ta có: \({W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}.100.{({4.10^{ - 2}})^2} = 0,08J\) Đáp án: B
Câu 3 :
Động năng trong dao động điều hoà biển đổi theo thời gian
Đáp án : D Lời giải chi tiết :
Động năng trong dao động điều hoà biển đổi theo thời gian tuần hoàn với chu kỳ T/2 Đáp án: D
Câu 4 :
Một vật nhỏ dao động điều hòa dọc theo trục Ox. Khi vật cách vị trí cân bằng một đoạn 2 cm thì động năng của vật là 0,48 J. Khi vật cách vị trí cân bằng một đoạn 6 cm thì động năng của vật là 0,32 J. Biên độ dao động của vật bằng
Đáp án : C Lời giải chi tiết :
Theo định luật bảo toàn cơ năng, ta có: Cơ năng của vật ở cách vị trí cân bằng một đoạn 2 cm bằng Cơ năng của vật ở cách vị trí cân bằng một đoạn 6 cm. Wx1 = 0,02 = Wx2 = 0,06 => wđx1 + wtx1 = wđx2 + wtx2 \( \Rightarrow 0,48 + \frac{1}{2}kx_1^2 = 0,32 + \frac{1}{2}kx_2^2\) \( \Rightarrow 0,48 + \frac{1}{2}k.0,{02^2} = 0,32 + \frac{1}{2}k.0,{06^2}\) => k = 100 N/m => Cơ năng của vật là: \(W = 0,48.\frac{1}{2}.100.0,{02^2} = 0,5J\) Mà \(W = \frac{1}{2}k{A^2} \Rightarrow A = \sqrt {\frac{{2W}}{k}} = \sqrt {\frac{{2.0,5}}{{100}}} = 0,1m = 10cm\) Đáp án C
Câu 5 :
Một vật dao động điều hoà với chu kỳ T, động năng của vật biến đổi theo thời gian
Đáp án : D Lời giải chi tiết :
Động năng của vật biến đổi tuần hoàn theo thời gian với chu kỳ T/2 (xem lại phần lí thuyết) Đáp án: D
Câu 6 :
Trong dao động điều hòa của một vật thì tập hợp ba đại lượng nào sau đây là không thay đổi theo thời gian
Đáp án : C Lời giải chi tiết :
Năng lượng được bảo toàn nên không đổi, biên độ và tần số không đổi Đáp án: C
Câu 7 :
Một vật có khối lượng m dao động điều hòa với biên độ A. Khi chu kì tăng 3 lần thì năng lượng của vật sẽ
Đáp án : B Lời giải chi tiết :
Năng lượng của vật là \(W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}m{\left( {\frac{{2\pi }}{T}} \right)^2}{A^2}\) Do đó, khi chu kì tăng 3 lần thì năng lượng giảm \({3^2} = 9\) lần. Đáp án: B
Câu 8 :
Một chất điểm dao động điều hòa không ma sát. Khi vừa ra khỏi vị trí cân bằng một đoạn S, động năng của chất điểm là 1,8 J. Đi tiếp một đoạn S nữa thì động năng chỉ còn 1,5 J và nếu đi thêm một đoạn S nữa thì động năng bây giờ là? Biết rằng vật chưa đổi chiều chuyển động.
Đáp án : B Lời giải chi tiết :
Muốn tính động năng tại vị trí đó thì ta cần tính thế năng tại vị trí đó và cơ năng. Vì vật chưa đổi chiều chuyển động và thế năng tỉ lệ thuận với bình phương li độ nên \(\left\{ \begin{array}{l}\left| {{x_1}} \right| = S\\\left| {{x_2}} \right| = 2S\\\left| {{x_3}} \right| = 3S\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{W_{{t_2}}} = 4{W_{{t_1}}}\\{W_{{t_3}}} = 9{W_{{t_1}}}\end{array} \right.\) Bảo toàn năng lượng ta có
Đáp án B.
Câu 9 :
Trong dao động điều hòa, ở vị trí nào thì động năng của con lắc có giá trị gấp n lần thế năng?
Đáp án : C Lời giải chi tiết :
Muốn tìm li độ ta cần biết thế năng, do đó từ giả thiết ta sẽ thay vào biểu thức bảo toàn cơ năng để rút \({W_t}\) theo W từ đó tính được x theo A. Thật vậy, ta có
Đáp án C.
Câu 10 :
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hoà là sai?
Đáp án : C Lời giải chi tiết :
C sai. Tốc độ của vật đạt giá trị cực đại khi vật ở vị trí cân bằng. Ở vị trí cân bằng, thế năng bằng 0. Đáp án: C
Câu 11 :
Hai con lắc lò xo giống hệt nhau đặt trên cùng mặt phẳng nằm ngang. Con lắc thứ nhất và con lắc thứ hai dao động điều hòa cùng pha với biên độ lần lượt là 3A và A. Chọn mốc thế năng của mỗi con lắc tại vị trí cân bằng của nó. Khi động năng của con lắc thứ nhất là 0,72 J thì thế năng của con lắc thứ hai là 0,24 J. Khi thế năng của con lắc thứ nhất là 0,09 J thì động năng của con lắc thứ hai là
Đáp án : A Lời giải chi tiết :
Vì hai dao động điều hòa cùng pha nên ta luôn có \(\left\{ \begin{array}{l}\frac{{\left| {{x_1}} \right|}}{{\left| {{x_2}} \right|}} = \frac{{{A_1}}}{{{A_2}}} = 3\\\frac{{\left| {{v_1}} \right|}}{{\left| {{v_2}} \right|}} = \frac{{\omega {A_1}}}{{\omega {A_2}}} = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{W_{{t_1}}} = 9{W_{{t_2}}}\\{W_{{d_1}}} = 9{W_{{d_2}}}\end{array} \right.\)
Đáp án A.
|














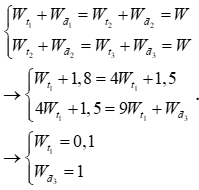
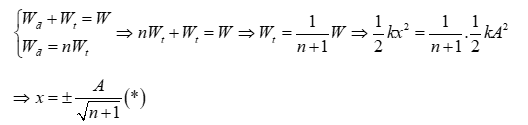
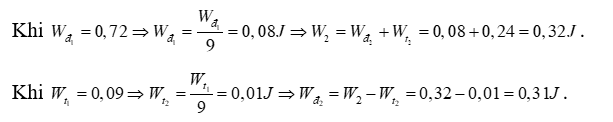





Danh sách bình luận