Trả lời câu hỏi 2 Bài 3 trang 72 SGK Toán 8 Tập 1Cho hình 24. Quảng cáo
Video hướng dẫn giải Cho hình \(24.\)
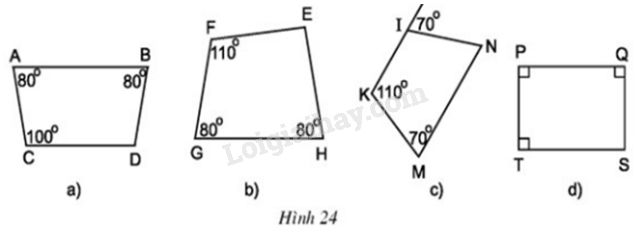
LG a. Tìm các hình thang cân. Phương pháp giải: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Lời giải chi tiết: +) Xét tứ giác \(ABCD\) có \(\widehat A+\widehat C=80^0+100^0=180^0\) mà hai góc này ở vị trí trong cùng phía nên \(AB//CD\). Do đó \(ABCD\) là hình thang. Lại có \(\widehat A=\widehat B=80^0\) nên hình thang \(ABCD\) là hình thang cân. +) Xét tứ giác \(EFGH\) không có cặp cạnh nào song song nên không là hình thang +) Xét tứ giác \(KINM\) có \(\widehat K+\widehat M=110^0+70^0=180^0\) mà hai góc này ở vị trí trong cùng phía nên \(KI//MN\). Do đó \(KINM\) là hình thang. Lại có \(\widehat I+70^0=180^0\) (hai góc kề bù) nên \(\widehat I=180^0-70^0=110^0\) Suy ra \(\widehat I=\widehat K\) nên \(KINM\) là hình thang cân. +) Xét tứ giác \(PQST\) có \(PQ\bot PT, ST\bot PT\) nên \(QP//ST\). Do đó \(PQST\) là hình thang. Lại có: \(\widehat P=\widehat Q=90^0\) nên \(PQST\) là hình thang cân. Vậy có các hình thang cân là: \(ABDC, IKMN, PQST\) LG b. Tính các góc còn lại của mỗi hình thang cân đó. Phương pháp giải: Áp dụng: Định lí tổng các góc của một tứ giác. Lời giải chi tiết: +) Hình thang cân \(ABCD\) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(ABCD\) ta có: \(\eqalign{ +) Hình thang cân \(IKMN\) \( \widehat I = {110^o}\) (theo câu a) \(\widehat N = {70^o}\) (hai góc so le trong) +) Hình thang cân \(PQST\) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(PQST\) ta có: \(\eqalign{ LG c. Có nhận xét gì về hai góc đối của hình thang cân? Phương pháp giải: Hai góc kề bù có tổng số đo bằng \(180^o\). Lời giải chi tiết: Hai góc đối của hình thang cân bù nhau. Loigiaihay.com
|




















Danh sách bình luận