Trả lời câu hỏi 1 Bài 6 trang 84 Toán 9 Tập 2

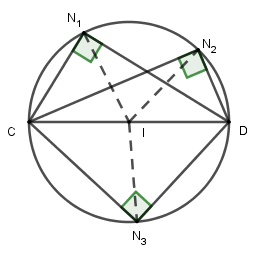
Đề bài

Cho đoạn thẳng \(CD\).

a) Vẽ ba điểm \(N_1;N_2;N_3\) sao cho \( \widehat {CN_1D}=\widehat {CN_2D}=\widehat {CN_3D}=90^0\)

b) Chứng minh rằng các điểm \(N_1;N_2;N_3\) nằm trên đường tròn đường kính \(CD.\)

Lời giải chi tiết

a) Vẽ hình.

b) Gọi \(I\) là trung điểm cạnh \(CD.\)

Cách 1:

Vì tam giác \(C{N_1}D\) vuông tại \({N_1}\) nên \(I{N_1} = IC = ID = \dfrac{{CD}}{2}\) ( đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Tương tự với hai tam giác vuông \(C{N_2}D;C{N_3}D\) ta có \(I{N_2} = I{N_3} = IC = ID = \dfrac{{CD}}{2}\)

Vậy \(I{N_1} = I{N_2} = I{N_3} = \dfrac{{CD}}{2}\)  hay \({N_1};{N_2};{N_3}\) thuộc đường tròn đường kính \(CD.\)

Cách 2: 

Vì \(\widehat{C{N_1}D} = 90^0\) nên \(\widehat{C{N_1}D}\) là góc nội tiếp chắn nửa đường tròn đường kính CD. Do đó, \(N_{1}\) nằm trên đường tròn đường kính CD.

Tương tự, \(N_{2}, N_{3}\) nằm trên đường tròn đường kính CD.

Vậy \({N_1};{N_2};{N_3}\) thuộc đường tròn đường kính \(CD.\)