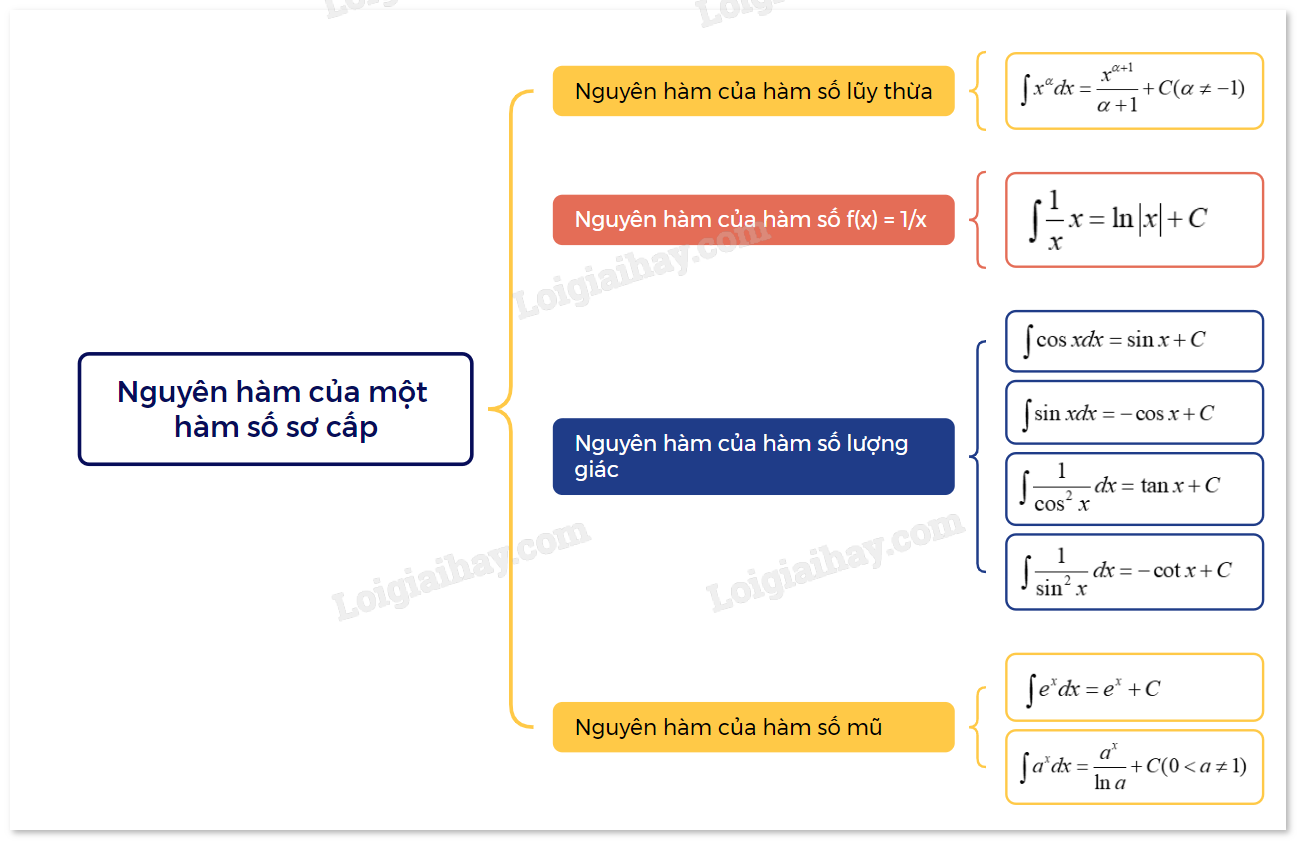
Lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều1. Nguyên hàm của hàm số lũy thừa Hàm số lũy thừa (y = {x^alpha }(alpha in R)) có đạo hàm với mọi x > 0 và (({x^alpha })' = alpha {x^{alpha - 1}}) (int {{x^alpha }dx = frac{{{x^{alpha + 1}}}}{{alpha + 1}} + C(alpha ne - 1)} ) Quảng cáo
1. Nguyên hàm của hàm số lũy thừa
2. Nguyên hàm của hàm số \(f(x) = \frac{1}{x}\)
3. Nguyên hàm của hàm số lượng giác
4. Nguyên hàm của hàm số mũ
|




















Danh sách bình luận