Lý thuyết Lôgarit - Toán 11 Kết nối tri thức

1. Khái niệm Lôgarit

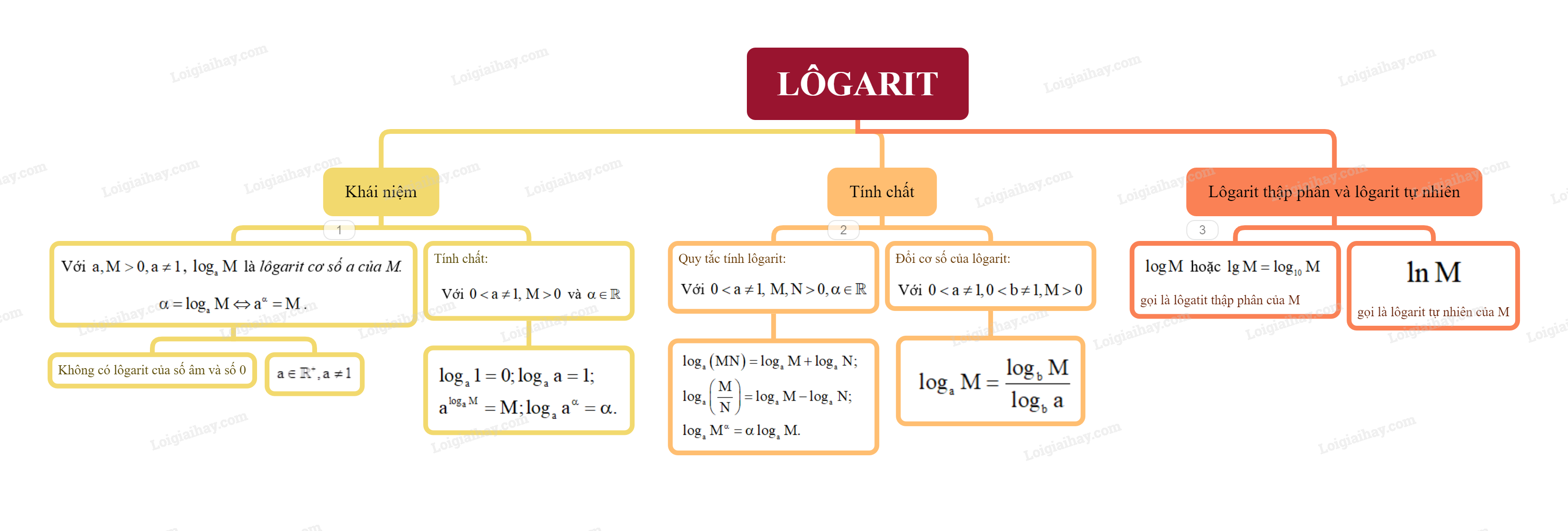
Cho a là một số thực dương khác 1 và M là một số thực dương. Số thực \(\alpha \) để \({a^\alpha } = M\) được gọi là lôgarit cơ số a của M và kí hiệu là \({\log _a}M\).

\(\alpha  = {\log _a}M \Leftrightarrow {a^\alpha } = M\).

Chú ý: Không có lôgarit của số âm và số 0. Cơ số của lôgarit phải dương và khác 1. Từ định nghĩa lôgarit, ta có các tính chất sau:

Với \(0 < a \ne 1,\,\,M > 0\) và \(\alpha \) là số thực tùy ý, ta có:

\(\begin{array}{l}{\log _a}1 = 0;{\log _a}a = 1;\\{a^{{{\log }_a}M}} = M;{\log _a}{a^\alpha } = \alpha .\end{array}\)

2. Tính chất của lôgarit

a) Quy tắc tính lôgarit

Giả sử a là số thực dương khác 1, M và N là các số thực dương, \(\alpha \) là số thực tùy ý. Khi đó:

\(\begin{array}{l}{\log _a}\left( {MN} \right) = {\log _a}M + {\log _a}N;\\{\log _a}\left( {\frac{M}{N}} \right) = {\log _a}M - {\log _a}N;\\{\log _a}{M^\alpha } = \alpha {\log _a}M.\end{array}\)

b) Đổi cơ số của lôgarit

Với các cơ số lôgarit a và b bất kì (\(0 < a \ne 1,0 < b \ne 1\)) và M là số thực dương tùy ý, ta luôn có:

\({\log _a}M = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\).

3. Lôgarit thập phân và lôgarit tự nhiên

a) Lôgarit thập phân

Lôgarit cơ số 10 của một số dương M gọi là lôgatit thập phân của M, kí hiệu là \(\log M\) hoặc \(\lg M\) (đọc là lốc của M).

b) Số e và lôgarit tự nhiên

Lôgarit cơ số e của một số dương M gọi là lôgarit tự nhiên của M, kí hiệu là \(\ln M\) (đọc là lôgarit Nêpe của M).