Lý thuyết liên hệ giữa dây và khoảng cách từ tâm đến dâyTrong một đường tròn: Hai dây bằng nhau thì cách đều tâm. Hai dây cách đều tâm thì bằng nhau. Quảng cáo
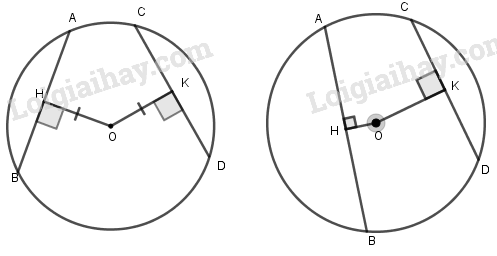
Liên hệ giữa dây và khoảng cách từ tâm đến dây Định lý 1: Trong một đường tròn: a) Hai dây bằng nhau thì cách đều tâm. b) Hai dây cách đều tâm thì bằng nhau. Định lý 2. Trong hai dây của một đường tròn: a) Dây nào lớn hơn thì dây đó gần tâm hơn. b) Dây nào gần tâm hơn thì dây đó lớn hơn.
Xét đường tròn (O): \(\begin{array}{l}OH \bot AB\left( {H \in AB} \right)\\OK \bot CD\left( {K \in CD} \right)\end{array}\) Khi đó: \(\begin{array}{l}AB = CD \Leftrightarrow OH = OK\\AB > CD \Leftrightarrow OH < OK\end{array}\) CÁC DẠNG TOÁN THƯỜNG GẶP So sánh hai đoạn thẳng Phương pháp: Ta thường sử dụng các kiến thức sau: - Trong một đường tròn: + Hai dây bằng nhau thì cách đều tâm. + Hai dây cách đều tâm thì bằng nhau. - Trong hai dây của một đường tròn: + Dây nào lớn hơn thì dây đó gần tâm hơn. + Dây nào gần tâm hơn thì dây đó lớn hơn, - Chứng minh hai tam giác bằng nhau, quan hệ giữa các yếu tố trong tam giác.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
