Lý thuyết hai đường thẳng vuông góc1. Tích vô hướng của hai vectơ trong không gian. Quảng cáo
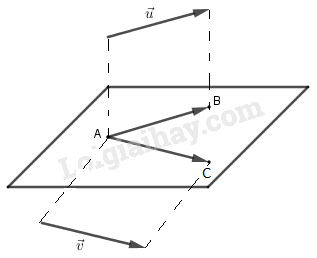
1. Tích vô hướng của hai vectơ trong không gian. - Góc giữa hai véctơ trong không gian: Góc giữa hai vectơ (khác véctơ không) \(\vec{u},\vec{v}\) là góc \(\widehat {BAC}\) với \(\vec{AB}=\vec{u}\); \(\vec{AC}=\vec{v}\)
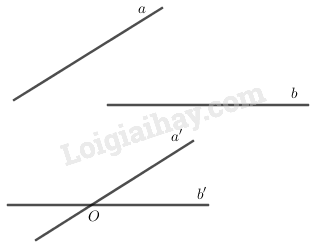
- Tích vô hướng của hai vectơ trong không gian: Cho hai vectơ khác vectơ không \(\vec{u},\vec{v}\) : Biểu thức \(\vec{u}.\vec{v}=|\vec{u}|.|\vec{v}|.cos(\vec{u},\vec{v})\) được gọi là tích vô hướng của hai vectơ \(\vec{u}\) và \(\vec{v}\) Nếu \(\vec{u}\) = \(\vec{0}\) hoặc \(\vec{v}\) = \(\vec{0}\) thì ta quy ước \(\vec{u}\) . \(\vec{v}\) = \(\vec{0}\). 2. Vectơ chỉ phương của đường thẳng. - Vectơ \(\vec{a} \ne \vec{0} \) là véctơ chỉ phương của đường thẳng \(d\) nếu giá của \(\vec{a}\) song song hoặc trùng với \(d\). - Nếu \(\vec{a}\) là vectơ chỉ phương của đường thẳng \(d\) thì k\(\vec{a}\) (\(k ≠ 0\)) cũng là vectơ chỉ phương của d. 3. Góc giữa hai đường thẳng trong không gian. Định nghĩa: Góc giữa hai đường thẳng \(a\) và \(b\) trong không gian là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song với \(a\) và \(b\) Nhận xét: - Ta có thể lấy điểm \(O\) thuộc một trong hai đường thẳng \(a\) và \(b\), rồi vẽ một đường thẳng qua \(O\) và song song với đường thẳng còn lại. - Nếu \(\vec{u_{1}},\vec{u_{2}}\) lần lượt là vectơ chỉ phương của \(a\) và \(b\) và (\(\vec{u_{1}},\vec{u_{2}}) = α\) thì: + góc \((a; b) = α\) nếu \(0^0 ≤ α ≤ 90^0\) + góc \((a; b) = 180^0- α\) nếu \( 90^0 < α ≤ 180^0\). - Nếu \(a//b\) hoặc \(a \equiv b\) thì \(\widehat {\left( {a,b} \right)} = {0^0}\) 4. Hai đường thẳng vuông góc với nhau. a) Định nghĩa: Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \(90^0\) b) Nhận xét: - Nếu\(\vec{u_{1}},\vec{u_{2}}\) lần lượt là các VTCP của \(a\) và \(b\) thì: \(a ⊥ b ⇔ \vec{u_{1}}.\vec{u_{2}}= 0\). - Nếu \(\left\{ \begin{array}{l} - Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau. c) Một số dạng toán thường gặp Dạng 1: Tính góc giữa hai đường thẳng. Phương pháp 1: Sử dụng định lý hàm số cô sin hoặc tỉ số lượng giác. \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\) Phương pháp 2: Sử dụng công thức tính cô sin góc giữa hai đường thẳng biết hai véc tơ chỉ phương của chúng. $\cos \varphi = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right| = \dfrac{{\left| {\overrightarrow u .\overrightarrow v } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}$ Để tính \(\overrightarrow u ,\overrightarrow v ,\left| {\overrightarrow u } \right|,\left| {\overrightarrow v } \right|\) ta chọn ba véc tơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng mà có thể tính được độ dài và góc giữa chúng, sau đó biểu thị các véc tơ \(\overrightarrow u ,\overrightarrow v \) qua các véc tơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) rồi thực hiện các tính toán. Dạng 2: Chứng minh hai đường thẳng vuông góc. Phương pháp: Để chứng minh hai đường thẳng \({d_1},{d_2}\) vuông góc ta thực hiện một trong các cách: Cách 1: Chứng minh \(\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 0\), trong đó \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) là các VTCP của \({d_1},{d_2}\). Cách 2: Sử dụng tính chất \(\left\{ \begin{array}{l}b//c\\a \bot c\end{array} \right. \Rightarrow a \bot b\) Cách 3: Sử dụng định lý Pi-ta-go hoặc xác định góc giữa \({d_1},{d_2}\) và tính trực tiếp góc đó.
|




















Danh sách bình luận