Lý thuyết góc tạo bởi tia tiếp tuyến và dây cung1. Định nghĩa Quảng cáo
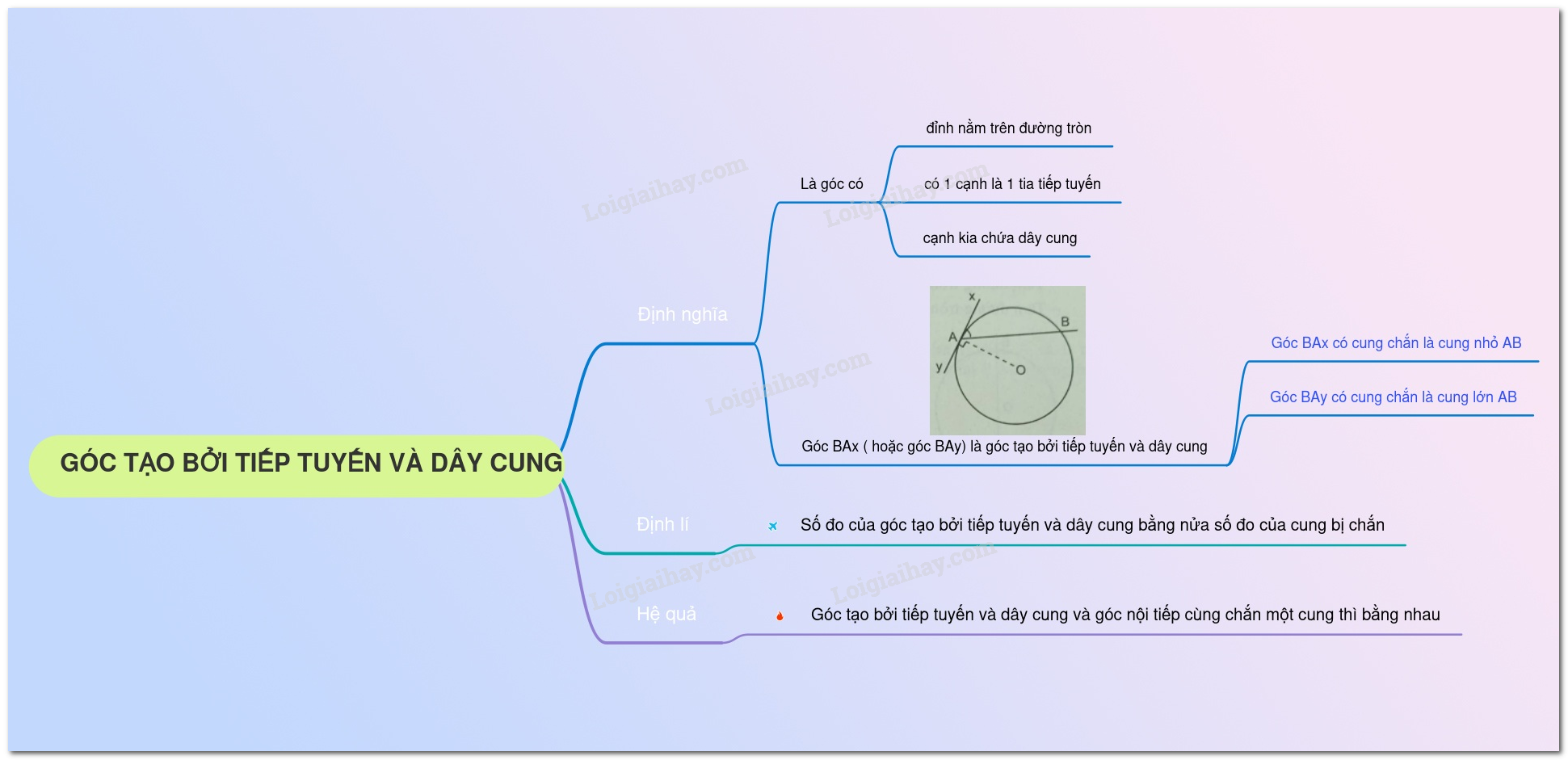
1. Các kiến thức cần nhớ Góc tạo bởi tia tiếp tuyến và dây cung Định nghĩa: Cho đường tròn tâm \((O)\) có \(Ax\) là tia tiếp tuyến tại tiếp điểm $A$ và dây cung $AB.$ Khi đó, góc \(BAx\) là góc tạo bởi tia tiếp tuyến và dây cung. Ví dụ : Góc \(BAx\) (hình $1$) là góc tạo bởi tia tiếp tuyến \(Ax\) và dây cung \(AB\) .  Định lý: Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. Ví dụ: Số đo góc \(BAx\) (hình $1$) bằng nửa số đo cung nhỏ \(AB.\)  Hệ quả: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau. Ví dụ : \(\widehat {BAx} = \widehat {ACB}\) (hình $2$)  2. Các dạng toán thường gặp Dạng 1: Chứng minh các góc bằng nhau, các tam giác đồng dạng, các hệ thức về cạnh Phương pháp: Ta sử dụng hệ quả về góc tạo bởi tia tiếp tuyến và dây cung hoặc hệ quả của hai góc nội tiếp: " Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau." Dạng 2: Chứng minh các đường thẳng vuông góc, song song. Chứng minh một tia là tiếp tuyến của đường tròn. Tính độ dài bán kính, độ dài đoạn thẳng Phương pháp: Sử dụng hệ quả về góc tạo bởi tia tiếp tuyến và dây cung hoặc hệ quả của hai góc nội tiếp. Sử dụng hệ thức lượng trong tam giác vuông và định lý Pytago.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
