Lý thuyết cung chứa góc

1. Các kiến thức cần nhớ 

Với đoạn thẳng $AB$ và góc $\alpha$ $\left( {0^\circ  < \alpha  < 180^\circ } \right)$ cho trước thì quỹ tích các điểm $M$ thỏa mãn $\widehat {AMB} = \alpha$ là hai cung chứa góc $\alpha$ dựng trên đoạn $AB$.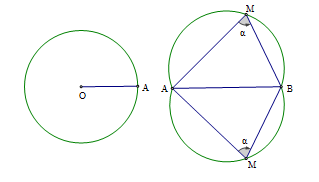

Chú ý : Hai cung chứa góc $\alpha$ nói trên là hai cung tròn đối xứng nhau qua $AB$. Hai điểm $A,B$ được coi là thuộc quỹ tích.

b. Cách vẽ cung chứa góc

Bài toán: Cho đoạn thẳng $AB$ và góc $\alpha \,({0^0} < \alpha  < {180^0}).$ Tìm tập hợp các điểm $M$ thoả mãn $\widehat {AMB} = \alpha$ .

- Vẽ đường trung trực $d$ của đoạn thẳng $AB$ ;

- Vẽ tia $Ax$ tạo với $AB$ một góc $\alpha$;

- Vẽ đường thẳng $Ay$ vuông góc với $Ax$. Gọi $O$ là giao điểm của $Ay$ với $d$.

- Vẽ cung $\overparen{AmB}$ , tâm $O$ , bán kính $OA$ sao cho cung này nằm ở nửa mặt phẳng bờ $AB$ không chứa tia $A\,x$. Cung $\overparen{AmB}$ được vẽ như trên là một cung chứa góc $\alpha$.

c. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm $M$ thỏa mãn tính chất $T$ là một hình $H$ nào đó, ta phải chúng minh hai phần :

Phần thuận : Mọi điểm có tính chất $T$ đều thuộc hình $H$.

Phần đảo : Mọi điểm thuộc hình $H$ đều có tính chất $T$.

Từ đó đi đến kết luận quỹ tích các điểm $M$ có tính chất $T$ là hình $H$.

(Thông thường với bài toán: “Tìm quỹ tích …” ta nên dự đoán hình $H$ trước khi chứng minh)

2. Các dạng toán thường gặp

Dạng 1 : Quỹ tích là cung chứa góc $\alpha$ .

Phương pháp :

- Tìm đoạn cố định trong hình vẽ.

- Nối điểm phải tìm với hai đầu đoạn thẳng cố định đó, xác định góc $\alpha$ không đổi.

- Khẳng định điểm phải tìm quỹ tích thuộc cung chứa góc $\alpha$dựng trên đoạn cố định.

Dạng 2 : Chứng minh nhiều điểm thuộc đường tròn

Phương pháp :

Chứng minh nhiều điểm cùng thuộc nửa mặt phẳng bờ là$AB$và cùng nhìn đoạn cố định $AB$ dưới một góc không đổi.

Dạng 3 : Dựng cung chứa góc

Phương pháp :

Thực hiện quy trình dựng sau đây :

+ Vẽ đường trung trực $d$ của đoạn thẳng $AB$;

+ Vẽ tia $A\,x$ tạo với $AB$ một góc $\alpha$;

+ Vẽ đường thẳng $Ay$ vuông góc với $A\,x$. Gọi $O$ là giao điểm của $Ay$ với $d$.

+ Vẽ cung $AmB$ , tâm $O$, bán kính $OA$ sao cho cung này nằm ở nửa mặt phẳng bờ $AB$ không chứa tia $A\,x$. Cung $AmB$ được vẽ  như trên là một cung chứa góc $\alpha$.