Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo

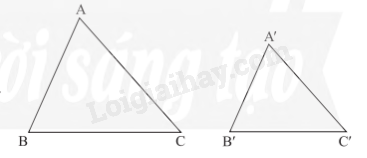
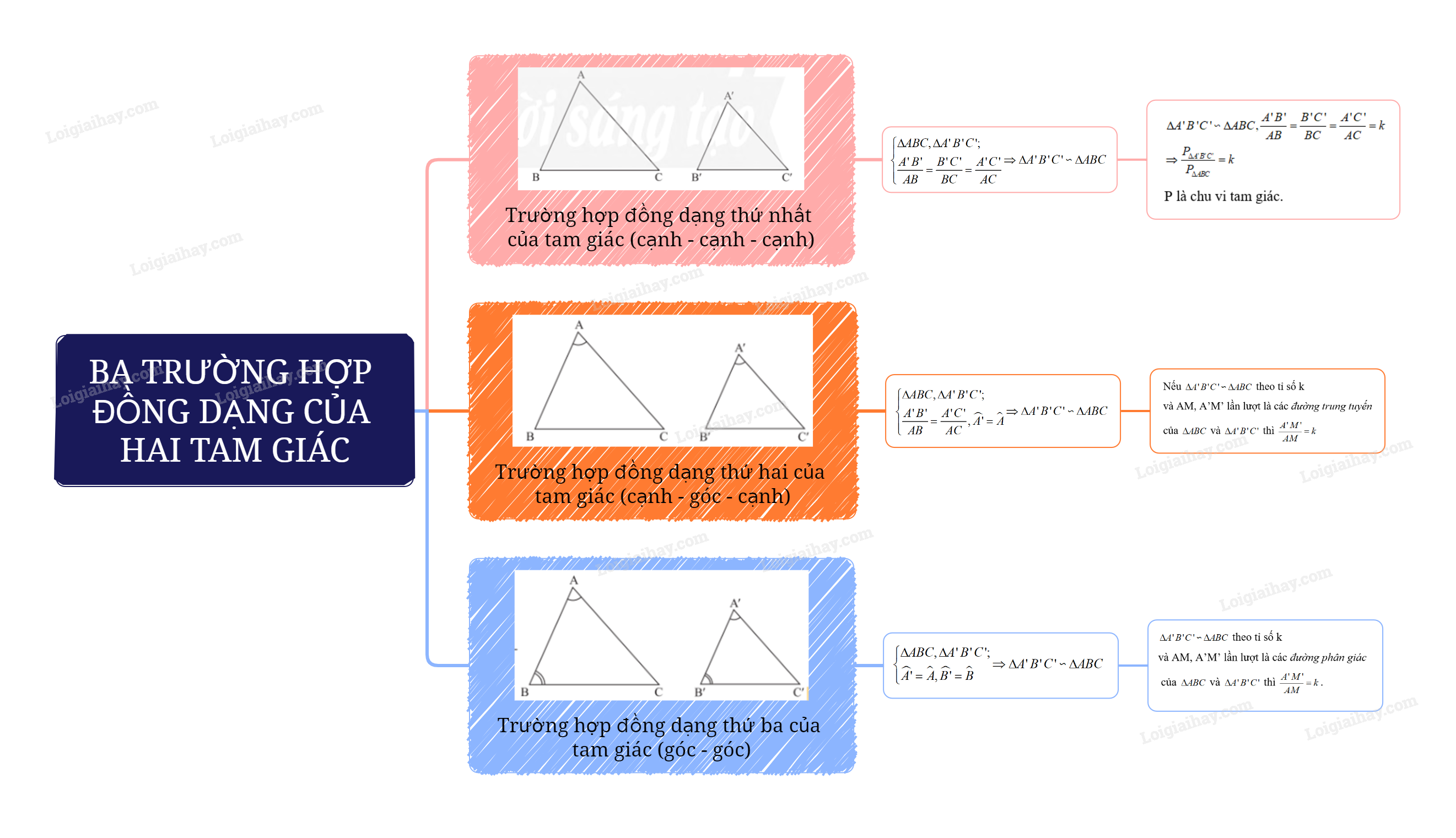
1. Trường hợp đồng dạng thứ nhất (Cạnh – cạnh – cạnh)

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

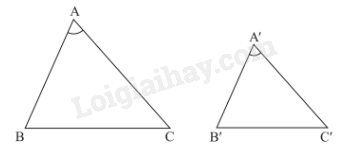
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.c.c)\end{array}\)

Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số chu vi của hai tam giác đó cũng bằng k.

2. Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh)

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.

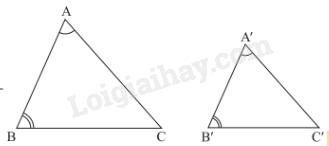
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.g.c)\end{array}\)

Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.

3. Trường hợp đồng dạng thứ ba (góc – góc)

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\widehat {A'} = \widehat A,\widehat {B'} = \widehat B\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\end{array}\)

Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số hai đường phân giác tương ứng của hai tam giác đó cũng bằng k.