Hoạt động 4 trang 125 Tài liệu dạy – học Toán 9 tập 1Giải bài tập Cho đường tròn (O) và hai dây AB, CD khác đường kính. Quảng cáo
Đề bài
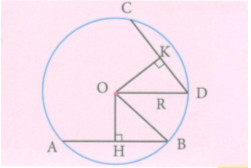
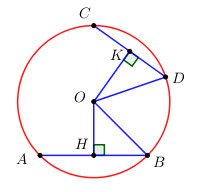
Cho đường tròn (O) và hai dây AB, CD khác đường kính. Từ O hạ OH và OK theo thứ tự vuông góc với AB và CD. Hãy điền vào chỗ chấm (…) để chứng minh : Nếu AB = CD thì OH = OK. Xét hai tam giác vuông OHB và OKD, ta có : OB = OD (…………..) HB = KD (…………..) Suy ra \(\Delta OHB = \Delta OKD\) Do đó OH = OK. Lời giải chi tiết Xét hai tam giác vuông OHB và OKD có: \(OB = OD\) (cùng bằng bán kính của \(\left( O \right)\)) \(HB = KD\) (do \(HB = \dfrac{1}{2}AB,\,\,KD = \dfrac{1}{2}CD,\)\(\,\,AB = CD\,\,\left( {gt} \right)\)) Suy ra \(\Delta OHB = \Delta OKD\) (cạnh góc vuông – cạnh huyền) Do đó \(OH = OK\) (2 cạnh tương ứng) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
