Bài 9. Chuyển động thẳng biến đổi đều trang 15, 16, 17 SBT Vật lí 10 Kết nối tri thức với cuộc sốngChuyển động nào sau đây không phải là chuyển động thẳng biến đổi đều? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
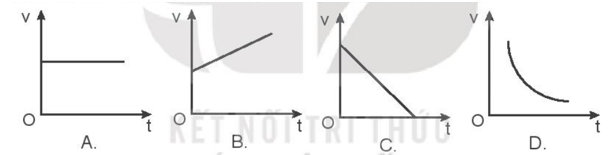
9.1 Chuyển động nào sau đây không phải là chuyển động thẳng biến đổi đều? A. Viên bi lăn xuống trên máng nghiêng. B. Vật rơi từ trên cao xuống đất. C. Hòn đá bị ném theo phương nằm ngang. D. Quả bóng được ném lên theo phương thẳng đứng. Phương pháp giải: Vận dụng kiến thức về đặc điểm của chuyển động thẳng biến đổi đều để nhận biết các loại chuyển động trong từng trường hợp. Lời giải chi tiết: A là chuyển động thẳng nhanh dần đều. B là chuyển động rơi tự do và cũng là chuyển động thẳng nhanh dần đều. C là chuyển động ném theo phương ngang có quỹ đạo không phải là đường thẳng và có sự kết hợp của nhiều loại chuyển động. D là chuyển động chậm dần đều. Chọn đáp án C. 9.2 Công thức liên hệ giữa độ dịch chuyển, vận tốc và gia tốc của chuyển động nhanh dần đều là A. \({v^2} - v_{_0}^2 = ad.\) B.\({v^2} - v_{_0}^2 = 2ad\) C. \(v - {v_0} = 2ad\) D.\({v_0}^2 - {v^2} = 2ad\) Phương pháp giải: Nhớ công thức liên hệ giữa độ dịch chuyển, vận tốc và gia tốc của chuyển động nhanh dần đều. Lời giải chi tiết: \({v^2} - v_{_0}^2 = 2ad\) Trong đó: + v0 là vận tốc tại thời điểm ban đầu. + v là vận tốc tại thời điểm t. + a: gia tốc của chuyển động. + d: độ dịch chuyển sau khoảng thời gian t. Chọn đáp án B. 9.3 Đồ thị nào sau đây là của chuyển động thẳng chậm dần đều?
Phương pháp giải: Vận dụng lý thuyết về chuyển động chậm dần đều để suy ra đặc điểm đồ thị. Lời giải chi tiết: Chuyển động thẳng chậm dần đều là chuyển động có quỹ đạo là đường thẳng và vận tốc giảm đều theo thời gian. A sai vì đồ thị có vận tốc không đổi theo thời gian. B sai vì đồ thị có vận tốc tăng đều theo thời gian. C đúng vì đồ thị có vận tốc giảm đều theo thời gian. D sai vì đồ thị dạng cong dốc xuống biểu thị vận tốc giảm nhưng không đều theo gian. Chọn đáp án C. 9.4 Chuyển động thẳng chậm dần đều có tính chất nào sau đây? A. Độ dịch chuyển giảm đều theo thời gian. B. Vận tốc giảm đều theo thời gian. C. Gia tốc giảm đều theo thời gian. D. Cả 3 tính chất trên. Phương pháp giải: Nắm vững lý thuyết về đặc điểm chuyển động chậm dần đều. Lời giải chi tiết: A sai vì chuyển động chậm dần nhưng độ dịch chuyển vẫn tăng chứ không phải giảm đều theo thời gian. B đúng vì chuyển động thẳng chậm dần đều là chuyển động có quỹ đạo là đường thẳng và vận tốc giảm đều theo thời gian. C sai vì trong chuyển động chậm dần đều gia tốc có độ lớn, hướng không đổi theo thời gian. Chọn đáp án B. 9.5
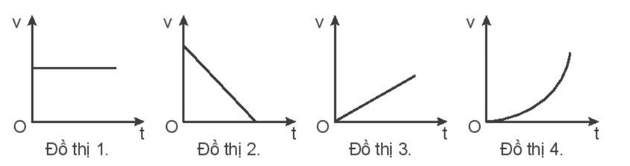
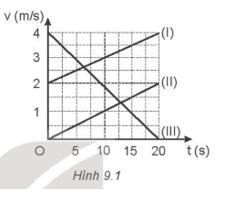
Các chuyển động sau đây có thể phù hợp với đồ thị nào trong bốn đồ thị trên? a) Chuyển động của ô tô khi thấy đèn giao thông chuyển sang màu đỏ. b) Chuyển động của vận động viên bơi lội khi có tín hiệu xuất phát. c) Chuyển động của vận động viên bơi lội khi bơi đều. d) Chuyển động của xe máy đang đứng yên khi người lái xe vừa tăng ga. Phương pháp giải: Nắm được đặc điểm và dạng đồ thị của các loại chuyển động, phân tích dữ kiện để xác định loại chuyển động và đồ thị phù hợp. Lời giải chi tiết: a) Khi thấy đèn giao thông chuyển sang màu đỏ, người điều khiển sẽ đạp phanh và ô tô sẽ chuyển động chậm dần đều => Đồ thị 2. b) Khi có tín hiệu xuất phát, vận động viên sẽ tăng vận tốc để bơi về đích => chuyển động nhanh dần đều => Đồ thị 3. c) Khi vận động viên bơi đều thì vận tốc không đổi theo thời gian => chuyển động thẳng đều => Đồ thị 1. d) Khi xe máy đang đứng yên người lái xe vừa tăng ga thì vận tốc xe sẽ tăng một cách đột ngột => Đồ thị 4. 9.6 Hình 9.1 là đồ thị vận tốc - thời gian của ba chuyển động thẳng biến đổi đều.
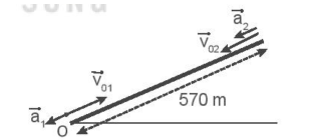
a) Viết công thức tính vận tốc và độ dịch chuyển của mỗi chuyển động. b) Tính độ dịch chuyển của chuyển động (III). Phương pháp giải: - Sử dụng cách đọc số liệu từ đồ thị: xác định v0 và v tại một thời điểm t bất kì. - Tính gia tốc của chuyển động: a = \(\frac{{\Delta v}}{{\Delta t}}\). - Sử dụng công thức tính vận tốc và độ dịch chuyển của chuyển động thẳng biến đổi đều: \(v = {v_0} + at\); \(d = {v_0}t + \frac{1}{2}a{t^2}\). Trong đó: + v0 là vận tốc tại thời điểm ban đầu. + v là vận tốc tại thời điểm t. + a là gia tốc của chuyển động. + d là độ dịch chuyển của chuyển động sau khoảng thời gian t. Lời giải chi tiết: a) Căn cứ vào đồ thị Hình 9.1 ta có thể xác định được: - Chuyển động (I) có: Vận tốc ban đầu: v01 = 2 m/s. Vận tốc tại t = 20 s là v = 4 m/s. Gia tốc của chuyển động là: a1 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{01}}}}{{\Delta t}}\)=\(\frac{{4 - 2}}{{20}}\)= 0,1 m/s2 Vận tốc của chuyển động là: \({v_1} = {v_{01}} + {a_1}t\)\( = \)\(2{\rm{ }} + {\rm{ }}0,1t\)(m/s). Độ dịch chuyển của chuyển động: \({d_1} = {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)\( = 2t + 0,05{t^2}\)(m). Tương tự, ta có: - Chuyển động (II) có: Vận tốc ban đầu: v02 = 0 m/s. Vận tốc tại t = 20 s là v = 2 m/s. Gia tốc của chuyển động là: a2 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{02}}}}{{\Delta t}}\)=\(\frac{{2 - 0}}{{20}}\)= 0,1 m/s2 Vận tốc của chuyển động là: \({v_2} = {v_{02}} + {a_2}t\)\( = \)\(0,1t\)(m/s). Độ dịch chuyển của chuyển động: \({d_2} = {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)\( = 0,05{t^2}\)(m). - Chuyển động (III) có: Vận tốc ban đầu: v03 = 4 m/s. Vận tốc tại t = 20 s là v = 0 m/s. Gia tốc của chuyển động là: a3 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{03}}}}{{\Delta t}}\)=\(\frac{{0 - 4}}{{20}}\)= -0,2 m/s2 Vận tốc của chuyển động là: \({v_3} = {v_{03}} + {a_3}t\)\( = \)\(4 - 0,2t\)(m/s). Độ dịch chuyển của chuyển động: \({d_3} = {v_{03}}t + \frac{1}{2}{a_3}{t^2}\)\( = 4t - 0,1{t^2}\)(m). b) Ta có độ dịch chuyển của chuyển động 3 sau 20 s chuyển động là: \({d_3} = {v_{03}}t + \frac{1}{2}{a_3}{t^2}\)\( = 4t - 0,1{t^2}\)\( = {\rm{ }}4.20{\rm{ }} - {\rm{ }}0,{1.20^2} = {\rm{ }}40{\rm{ }}m.\) 9.7 Một máy bay có vận tốc khi tiếp đất là 100 m/s. Để giảm vận tốc sau khi tiếp đất, máy bay chỉ có thể có gia tốc đạt độ lớn cực đại là 4 m/s2. a) Tính thời gian ngắn nhất để máy bay dừng hẳn kể từ khi tiếp đất. b) Máy bay này có thể hạ cánh an toàn ở sân bay có đường bay dài 1 km. hay không? Phương pháp giải: - Viết phương trình tính vận tốc và độ dịch chuyển của chuyển động thẳng biến đổi đều theo công thức: \(v = {v_0} + at\); \(d = {v_0}t + \frac{1}{2}a{t^2}\) Trong đó: + v0 là vận tốc tại thời điểm ban đầu. + v là vận tốc tại thời điểm t. + a là gia tốc của chuyển động. + d là độ dịch chuyển của chuyển động sau khoảng thời gian t. - Máy bay dừng hẳn khi v = 0 => tính thời gian để máy bay dừng. - Sau khi tính được thời gian, thế vào tính độ dịch chuyển rồi đưa ra kết luận. Lời giải chi tiết: a) Theo dữ liệu bài toán ta có: v0 = 100 m/s; a = -4 m/s2 Ta có phương trình vận tốc của máy bay là: \(v = {v_0} + at\)= 100 – 4t (m/s). Máy bay dừng hẳn khi v = 0 ⬄ 100 – 4t = 0 => t = \(\frac{{ - 100}}{{ - 4}}\)= 25 s. b) Ta có phương trình độ dịch chuyển của máy bay là: \(d = {v_0}t + \frac{1}{2}a{t^2}\)= 100t – 2t2 (m). Sau 25 s máy bay dịch chuyển thêm: d = 100.25 – 2.252 = 1250 m = 1,25 km. Vậy máy bay không thể hạ cánh an toàn trên sân bay có đường bay dài 1 km. 9.8 Một ô tô khi hãm phanh có thể có gia tốc 3 m/s2. Hỏi khi ô tô đang chạy với vận tốc là 72 km/h thì phải hãm phanh cách vật cản là bao nhiêu mét để không đâm vào vật cản? Thời gian hãm phanh là bao nhiêu? Phương pháp giải: - Vận dụng công thức liên hệ giữa vận tốc, gia tốc và độ dịch chuyển để tính độ dịch chuyển của ô tô sau khi hãm phanh: v2 – v02 = 2ad. - Từ công thức tính vận tốc v = v0 + at => t = \(\frac{{v - {v_0}}}{a}\). Lời giải chi tiết: Theo dữ liệu bài toán ta có: v0 = 72 km/h = 20 m/s; a = -3 m/s2; v = 0 km/h. Áp dụng công thức: v2 – v02 = 2ad => d = \(\frac{{{v^2} - v_0^2}}{{2a}}\)= \(\frac{{{0^2} - {{20}^2}}}{{2.( - 3)}}\)≈ 66,7 m. Vậy phải hãm phanh trước vật cản trên 66,7 m. Ta có: v = v0 + at => t = \(\frac{{v - {v_0}}}{a}\)= \(\frac{{0 - 20}}{{ - 3}}\)=\(\frac{{ - 20}}{{ - 3}}\)≈ 6,7 s. 9.9 Một người đi xe máy trên một đoạn đường thẳng muốn đạt được vận tốc 36 km/h sau khi đi được 100 m bằng một trong hai cách sau: Cách 1: Chạy thẳng nhanh dần đều trong suốt quãng đường. Cách 2: Chỉ cho xe chạy nhanh dần đều trên 1/5 quãng đường, sau đó cho xe chuyển động thẳng đều trên quãng đường còn lại. a) Hỏi cách nào mất ít thời gian hơn? b) Hãy tìm một cách khác để giải bài toán này. Phương pháp giải: a) - Tính thời gian chuyển động trong 2 cách để so sánh. - Cách 1: + Vận dụng công thức giữa vận tốc, gia tốc, độ dịch chuyển trong chuyển động nhanh dần đều để tính gia tốc chuyển động: v2 – v02 = 2ad. + Thế gia tốc tìm được vào công thức tính vận tốc để tìm thời gian chuyển động: v = v0 + at => t = \(\frac{{v - {v_0}}}{a}\). - Cách 2: + Tương tự cách 1 tính khoảng thời gian khi vật chuyển động nhanh dần đều. + Tính khoảng thời gian khi vật chuyển động thẳng dần đều. Sử dụng công thức: v = \(\frac{d}{t}\)=> t = \(\frac{d}{v}\). + Cộng 2 khoảng thời gian lại ta được thời gian vật chuyển động trong cách 2. b) Giải thích bằng cách tính vận tốc trung bình. Lời giải chi tiết: a) Cách 1: Theo đề bài có: v0 = 0; v = 36 km/h = 10 m/s; d = 100 m. Áp dụng công thức: v2 – v02 = 2ad => a = \(\frac{{{v^2} - v_0^2}}{{2d}}\)= \(\frac{{{{10}^2} - {0^2}}}{{2.100}}\)= 0,5 m/s2. Mà v = v0 + at => t = \(\frac{{v - {v_0}}}{a}\)= \(\frac{{10 - 0}}{{0,5}}\)= 20 s. Cách 2: Thời gian xe chuyển động nhanh dần đều: Theo đề bài có: v0 = 0; v = 36 km/h = 10 m/s; d1 = \(\frac{{100}}{5}\)= 20 m. Áp dụng công thức: v2 – v02 = 2a1d1 => a1 = \(\frac{{{v^2} - v_0^2}}{{2{d_1}}}\)= \(\frac{{{{10}^2} - {0^2}}}{{2.20}}\)= 2,5 m/s2. Mà v = v0 + a1t1 => t1 = \(\frac{{v - {v_0}}}{{{a_1}}}\)= \(\frac{{10 - 0}}{{2,5}}\)= 4 s. Thời gian xe chuyển động thẳng đều: v = \(\frac{{{d_2}}}{{{t_2}}}\)=> t2 = \(\frac{{{d_2}}}{v}\)=\(\frac{{100 - {d_1}}}{v}\)=\(\frac{{100 - 20}}{{10}}\)= 8 s. => Thời gian chuyển động trong cách 2 là: t’ = t1 + t2 = 4 + 8 = 12 m/s. b) Giải thích: Cách 1: Vật chuyển động thẳng nhanh dần đều trong suốt quãng đường => vtb1 = \(\frac{d}{t}\)= \(\frac{{100}}{{20}}\)= 5 m/s. Cách 2: Vật chuyển động thẳng nhanh dần đều và chuyển động thẳng đều => vtb2 = \(\frac{{{d_1} + {d_2}}}{{{t_1} + {t_2}}}\)\(\frac{{20 + 80}}{{4 + 8}}\)= \(\frac{{100}}{{12}}\)≈ 8,3 m/s Vậy vật chạy theo cách 2 sẽ có vận tốc trung bình lớn hơn cách 1 nên thời gian chuyển động cũng sẽ nhanh hơn. 9.10 Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s2. Cùng lúc đó, một ô tô đang chạy với vận tốc 20 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s2. Xác định vị trí hai xe gặp nhau trên dốc. Biết dốc dài 570 m. Phương pháp giải: Chọn chiều từ chân dốc lên đỉnh dốc là chiều dương. Điểm O là chân dốc như hình vẽ. Viết phương trình chuyển động của mỗi xe theo công thức: \(d = {d_0} + {v_0}t + \frac{1}{2}a{t^2}\) Hai xe gặp nhau khi d1 = d2. Giải phương trình ta sẽ xác định được vị trí 2 xe gặp nhau. Lời giải chi tiết: Chọn chiều từ chân dốc lên đỉnh dốc là chiều dương. Điểm O là chân dốc như hình vẽ.
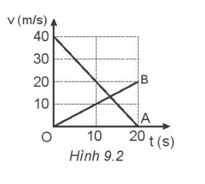
Xét chuyển động của ô tô, ta có: v01 = 20 m/s; a1 = -0,4 m/s2. => Phương trình chuyển động của ô tô: \({d_1} = {d_{01}} + {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)= 20t – 0,2t2. (1) Xét chuyển động của xe đạp, ta có: v02 = -2 m/s; d02 = 570 m; a2 = -0,2 m/s2. Phương trình chuyển động: \({d_2} = {d_{02}} + {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)= 570 – 2t – 0,1t2. (2) Khi ô tô và xe đạp gặp nhau: d1 = d2 => 20t – 0,2t2 = 570 – 2t – 0,1t2 (3) Nghiệm của phương trình (3) là t1 = 30 s và t2 = 190 s.\(\) Thế t1 vào (1) ta được d1 = 420 m. Thế t2 vào (2) ta được d2 = - 3400 m (Loại vì 2 xe gặp nhau trên dốc). Vậy 2 xe gặp nhau tại vị trí cách chân dốc 420 m. 9.11 Hai vật A và B chuyển động cùng chiều trên đường thẳng có đồ thị vận tốc – thời gian vẽ ở Hình 9.2. Biết ban đầu hai vật cách nhau 78 m.
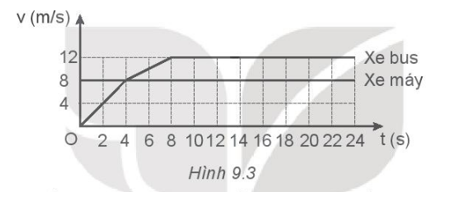
a) Hai vật có cùng vận tốc ở thời điểm nào? b) Viết phương trình chuyển động của mỗi vật. c) Xác định vị trí gặp nhau của hai vật. Phương pháp giải: a) Viết phương trình vận tốc của mỗi vật theo công thức: v = v0 + at Hai vật có cùng vật tốc khi vA = vB. Giải phương trình sẽ tìm được thời điểm hai vật có cùng vật tốc. b) Viết phương trình chuyển động của mỗi vật theo công thức: \(d = {d_0} + {v_0}t + \frac{1}{2}a{t^2}\). c) Hai vật gặp nhau khi dA = dB. Giải phương trình sẽ tìm được vị trí gặp nhau của 2 vật. Lời giải chi tiết: a) Từ đồ thị ta viết được phương trình vận tốc của mỗi vật như sau: vA = v0A + a1t = 40 – 2t (m/s). vB = v0B + a2t = t Hai vật có cùng vận tốc khi vA = vB ⬄ 40 – 2t = t ⬄ t = \(\frac{{40}}{3}\)≈13,3 s. b) Chuyển động A có: v01 = 40 m/s; a1 = \(\frac{{0 - 40}}{{20}}\)= -2 m/s2. => \({d_A} = {d_{01}} + {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)= 40t – t2 (1) - Chuyển động B có: v02 = 0 m/s; a2 = \(\frac{{10 - 0}}{{10}}\)= 1 m/s2. => \({d_B} = {d_{02}} + {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)= \(78 + \frac{1}{2}{t^2}\). (2) c) Hai vật gặp nhau khi dA = dB ⬄ 40t – t2 = \(78 + \frac{1}{2}{t^2}\) (3) Phương trình (3) cho hai nghiệm t = 2,12 s và t’ = 24,5 s Loại t’vì t’ lớn hơn 20 s. Thế t vào (1) ta được dA = 81,5 m. Vậy hai vật gặp nhau cách vị trí ban đầu của A 81,5 m. 9.12 Đồ thị vận tốc - thời gian trong Hình 9.3 là của một xe bus và một xe máy chạy cùng chiều trên một đường thẳng. Xe bus đang đứng yên, bắt đầu chuyển động thì xe máy đi tới.
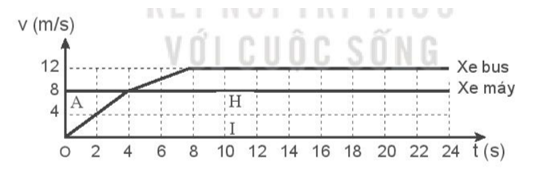
a) Tính gia tốc của xe bus trong 4 s đầu và trong 4 s tiếp theo. b) Khi nào thì xe bus bắt đầu chạy nhanh hơn xe máy? c) Khi nào thì xe bus đuổi kịp xe máy? d) Xe máy đi được bao nhiêu mét thì bị xe bus đuổi kịp? e) Tính vận tốc trung bình của xe bus trong 8 s đầu. Phương pháp giải: a) Sử dụng công thức tính gia tốc của chuyển động: a = \(\frac{{\Delta v}}{{\Delta t}}\). b) Xe bus chạy nhanh hơn xe máy khi vận tốc của xe bus lớn hơn vận tốc của xe máy. c) Viết phương trình chuyển động của mỗi xe theo công thức: Hai xe gặp nhau khi phương trình chuyển động của chúng bằng nhau. Giải phương trình sẽ tìm được thời gian chúng gặp nhau. d) Thế thời gian xe bus đuổi kịp xe máy vào phương trình chuyển động của xe máy sẽ tìm được quãng đường xe máy đã đi. e) Sử dụng công thức tính vận tốc trung bình: \({v_{tb}} = \frac{{\Delta d}}{{\Delta t}}\). + \(\Delta d\): Độ dịch chuyển trong khoảng thời gian \(\Delta t\). + \(\Delta t\): Thời gian chuyển động. Lời giải chi tiết:
a) Gia tốc của xe bus trong 4 s đầu là: a1 = \(\frac{{\Delta {v_1}}}{{\Delta {t_1}}}\)= \(\frac{{8 - 0}}{{4 - 0}}\)=\(\frac{8}{4}\)= 2 m/s2. Gia tốc của xe bus trong 4 s tiếp theo là: a2 = \(\frac{{\Delta {v_2}}}{{\Delta {t_2}}}\)= \(\frac{{12 - 8}}{{8 - 4}}\)=\(\frac{4}{4}\)= 1 m/s2. b) Từ đồ thị ta thấy sau giây thứ 4 thì đồ thị xe bus ở phí trên đồ thị xe máy => Vận tốc của xe bus lớn hơn vận tốc của xe máy. c) Gọi thời điểm hai xe gặp nhau là t. Đối với xe máy: Trong 8 s đầu: dm = vmtm = 8.8 = 56 m. Độ dịch chuyển của xe máy trong thời gian t là: dm = vmt = 8t Đối với xe bus: Trong 4 s đầu: \({d_1} = {v_{01}}{t_1} + \frac{1}{2}{a_1}{t_1}^2\)= 0 + \(\frac{1}{2}\).2.42 = 16 m. Trong 4 s tiếp theo: \({d_2} = {v_{02}}{t_2} + \frac{1}{2}{a_2}{t_2}^2\) = 8.4 + \(\frac{1}{2}\).1.42 = 40 m => Trong 8 s đầu xe bus đi được d1 + d2 = 56 m. => Trong 8 s đầu hai xe chưa gặp nhau. Độ dịch chuyển của xe bus trong thời gian t là: db = 56 + v3(t – 8) = 56 + 12(t -8) = 12t – 40. Hai xe gặp nhau khi dm = db ⬄ 8t = 12t – 40 => t = 10 s. Vậy hai xe gặp nhau tại thời điểm t = 10 s. d) Với t = 10 s => dm = 80 m Vậy xe bus đuổi kịp khi xe máy chạy được 80 m. e) Vận tốc trung bình của xe bus trong 8 s đầu là: \({v_{tb}} = \frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} + {d_2}}}{{{t_1} + {t_2}}}\)= \(\frac{{16 + 40}}{8}\)= 7 m/s.
|




















Danh sách bình luận