Bài 18. Lực ma sát trang 33, 34, 35 SBT Vật lí 10 Kết nối tri thức với cuộc sống

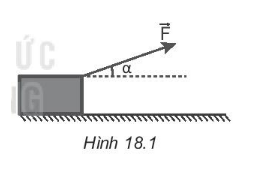
18.1

Một vật đang trượt trên một mặt phẳng, khi tốc độ của vật giảm thì hệ số ma sát giữa vật và mặt phẳng

A. giảm xuống.

B. không đổi.

C. tăng tỉ lệ với tốc độ của vật.

D.tăng tỉ lệ với bình phương tốc độ của vật.

Phương pháp giải:

Lý thuyết về hệ số ma sát trượt.

Lời giải chi tiết:

Tỉ số giữa độ lớn của lực ma sát trượt F_ms và áp lực N gọi là hệ số ma sát trượt, kí hiệu là μ.

Hệ số μ phụ thuộc vào vật liệu và tình trạng của hai mặt tiếp xúc, không phụ thuộc vào vận tốc của vật chuyển động. Do đó khi tốc độ của vật giảm thì hệ số ma sát giữa vật và mặt phẳng không đổi.

Chọn đáp án B.

18.2

Khi lực ép giữa hai mặt tiếp xúc tăng lên thì hệ số ma sát giữa hai mặt tiếp xúc

A. giảm đi.

B. tăng lên.

C. không thay đổi.

D. không xác định được.

Phương pháp giải:

Lý thuyết về hệ số ma sát trượt.

Lời giải chi tiết:

Tỉ số giữa độ lớn của lực ma sát trượt F_ms và áp lực N gọi là hệ số ma sát trượt, kí hiệu là μ.

Hệ số μ phụ thuộc vào vật liệu và tình trạng của hai mặt tiếp xúc, không phụ thuộc vào lực ép của tiếp xúc giữa hai vật. Do đó khi lực ép giữa hai mặt tiếp xúc tăng lên thì hệ số ma sát giữa hai mặt tiếp xúc không đổi.

Chọn đáp án B.

18.3

Một vật có khối lượng m trượt trên mặt phẳng ngang. Biết hệ số ma sát trượt giữa vật và mặt phẳng là μ, gia tốc trọng trường g. Biểu thức xác định lực ma sát trượt là

A. F_mst = μmg.                          B. F_mst = μg.

C. F_mst = μm.                            D. F_mst = mg.

Phương pháp giải:

Áp dụng công thức tính lực ma sát trượt: F_ms = μN.

Lời giải chi tiết:

Theo công thức tính lực ma sát trượt: F_ms = μN.

Mà một vật nằm trên mặt phẳng ngang thì N = P = mg.

=> F_mst = μmg.

Chọn đáp án A.

18.4

Một vận động viên môn hốc cây (khúc quân cầu) dùng gậy gạt quả bóng để truyền cho nó một tốc độ ban đầu 10 m/s. Hệ số ma sát giữa bóng và mặt băng là 0,10. Lấy g = 9,8 m/s². Quãng đường quả bóng đi được cho đến khi dừng lại là

A. 39 m.                                   B. 45 m.

C. 57 m.                                   D. 51 m.

Phương pháp giải:

Sử dụng công thức liên hệ giữa quãng đường, vận tốc và gia tốc để tính quãng đường bóng đi được đến khi dừng lại: \({v^2} - v_0^2 = 2as\).

Để tính a, ta sử dụng Định luật II Newton:\(\overrightarrow {{F_{ms}}}  = m\overrightarrow a \)

Lời giải chi tiết:

Theo định luật II Newton, ta có: \(\overrightarrow {{F_{ms}}}  = m\overrightarrow a \)

Mà F_ms = μN = μP = μmg.

Chọn chiều (+) là chiều chuyển động của quả bóng, chiếu lên chiều (+):

=> - F_ms = ma ó - μmg = ma => a = - μg = - 0,1.9,8 = -0,98 m/s²

Áp dụng công thức liên hệ giữa quãng đường, vận tốc và gia tốc:

 \({v^2} - v_0^2 = 2as\)=> s = \(\frac{{{v^2} - v_0^2}}{{2a}} = \frac{{0 - {{10}^2}}}{{2.( - 0,98)}}\) ≈ 51 m.

Vậy quãng đường quả bóng đi được cho đến khi dừng lại là 51 m.

Chọn đáp án D.

18.5

Một xe tải có khối lượng 3 tấn đang chuyển động trên đường nằm ngang, hệ số ma sát của xe tải với mặt đường là 0,1. Lấy g = 10 m/s² Độ lớn lực ma sát là

A. 3 000 N.           B. 30 000 N.          C. 300 N.              D. 30 N.

Phương pháp giải:

Áp dụng công thức tính lực ma sát trượt: F_ms = μN.

Lời giải chi tiết:

Theo đề bài ta có: m = 3 tấn = 3000 kg; μ = 0,1; g = 10 m/s².

Theo công thức tính lực ma sát trượt:

F_ms = μN = μP = μmg = 0,1.3000.10 = 3000 N.

Chọn đáp án A.

18.6

Một toa tàu có khối lượng 60 tấn chuyển động thẳng đều dưới tác dụng của lực kéo của đầu tàu theo phương nằm ngang F = 4,5.10⁴. Lấy g = 10 m/s. Hệ số ma sát giữa tàu và đường ray là

A. 0,075.               B.0,06.                 C. 0,15.                D. 0,015

Phương pháp giải:

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Vì toa tàu chuyển động thẳng đều nên a = 0 m/s².

Khi đó \(\overrightarrow {{F_k}}  = \overrightarrow { - {F_{mst}}} \)hay F_k = F_mst = = μ_tmg

Lời giải chi tiết:

Đổi m = 60 tấn = 60.10³ kg.

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Vì toa tàu chuyển động thẳng đều nên a = 0 m/s².

Khi đó \(\overrightarrow {{F_k}}  = \overrightarrow { - {F_{mst}}} \)hay F_k = F_mst = = μ_tmg.

=> \(\frac{{4,{{5.10}^4}}}{{{{6.10}^4}}}\)μ_t = \(\frac{{{F_k}}}{{mg}}\)= \(\frac{{4,{{5.10}^4}}}{{{{60.10}^4}}}\)= 0,075.

Chọn đáp án A.

18.7

Một cái hòm khối lượng m = 15 kg đặt trên sàn nhà. Người ta kéo hòm bằng một lực \(\overrightarrow F \) hướng chếch lên trên và hợp với phương nằm ngang một góc α = 20^o như Hình 18.1. Hòm chuyên động đều trên sàn nhà. Tính độ lớn của lực \(\overrightarrow F \). Biết hệ số ma sát trượt giữa hòm và sàn nhà là 0,3. Lấy g = 9,8 m/s².

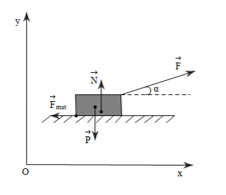
Phương pháp giải:

Hòm chịu tác dụng của các lực: lực kéo \(\overrightarrow F \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \)và lực ma sát trượt \({\overrightarrow F _{mst}}\).

Theo định luật II Newton, ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Vì hòm chuyển động đều nên a = 0 m/s² => \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = \overrightarrow 0 \).

Chọn hệ trục Oxy có chiều dương hướng lên (Oy), từ trái sang phải (Ox). Chiếu phương trình lần lượt lên trục Ox, Oy. Giải hệ phương trình.

Lời giải chi tiết:

Hòm chịu tác dụng của các lực: lực kéo \(\overrightarrow F \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \)và lực ma sát trượt \({\overrightarrow F _{mst}}\).

Theo định luật II Newton, ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Vì hòm chuyển động đều nên a = 0 m/s² => \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = \overrightarrow 0 \).

Chọn hệ trục Oxy có chiều dương hướng lên (Oy), từ trái sang phải (Ox) như hình vẽ. Chiếu phương trình lần lượt lên trục Ox, Oy. Ta được:

Chiếu xuống Ox:

F.cosα – F_mst = 0             (1)

Chiếu xuống Oy:

Fsinα – mg + N = 0         (2)

Ngoài ra: F_mst = μN         (3)

Từ (1), (2), (3) ta suy ra:

F = \(\frac{{\mu mg}}{{\cos \alpha  + \mu \sin \alpha }}\)= \(\frac{{0,3.15.9,8}}{{\cos {{20}^o} + 0,3.\sin {{20}^o}}}\)≈ 42,3 N.

18.8

Một ô tô có khối lượng 1,5 tấn chuyển động trên đường nằm ngang. Hệ số ma sát của xe với mặt đường là 0,01. Biết lực kéo gây ra bởi động cơ song song với mặt đường. Lấy g = 10 m/s². Xác định độ lớn của lực kéo để ô tô chuyển động nhanh dần đều với gia tốc 0,25 m/s².

Phương pháp giải:

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn chiều dương là chiều chuyển động của xe. Chiếu phương trình lên chiều dương, ta được: F_k – F_mst = ma => F_k = F_mst + ma

Mà F_mst = μN = μP = μmg.

Lời giải chi tiết:

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn chiều dương là chiều chuyển động của xe. Chiếu phương trình lên chiều dương, ta được: F_k – F_mst = ma => F_k = F_mst + ma

Mà F_mst = μN = μP = μmg.

=> F = ma + μmg = m(a + μg) = 1500(0,25 + 0,01.10) = 525 N.

18.9

Một mẩu gỗ có khối lượng m đặt trên mặt sàn nằm ngang. Người ta truyền cho nó một vận tốc tức thời 5 m/s. Tính thời gian để mầu gỗ dừng lại và quãng đường nó đi được tới lúc đó. Biết hệ số ma sát giữa mẩu gỗ và sàn nhà là 0,2 và lấy g= 10 m/s². Các đáp số tìm được có phụ thuộc vào khối lượng m không?

Phương pháp giải:

Theo định luật II Newton: \(\overrightarrow {{F_{mst}}}  = m\overrightarrow a \)

Chọn chiều (+) là chiều chuyển động của mẩu gỗ.

Khi đó: - F_mst = ma => a = \(\frac{{ - {F_{mst}}}}{m}\).

Để tính quãng đường đi được, ta áp dụng công thức độc lập thời gian:

v² – v₀² = 2as

Lại có v = v₀  + at => t = \(\frac{{v - {v_0}}}{a}\).

Lời giải chi tiết:

Theo định luật II Newton: \(\overrightarrow {{F_{mst}}}  = m\overrightarrow a \)

Mà F_mst = µN = μP= µmg.

Chọn chiều (+) là chiều chuyển động của mẩu gỗ.

Khi đó: - F_mst = ma => a = \(\frac{{ - {F_{mst}}}}{m}\)= - μg = - 0,2.10 = - 2 m/s².

Áp dụng công thức độc lập thời gian ta có: v² – v₀² = 2as

=> s = \(\frac{{{v^2} - v_0^2}}{{2a}}\)= \(\frac{{{0^2} - {5^2}}}{{2.( - 2)}}\)= 6,25 m.

Mặt khác có: v = v₀ + at => t = \(\frac{{v - {v_0}}}{a}\)= \(\frac{{0 - 5}}{{ - 2}}\)= 2,5 s.

Vậy thời gian để mầu gỗ dừng lại là 2,5 svà quãng đường nó đi được tới lúc đó là 6,25 m.

Kết quả tìm được không phụ thuộc vào m.

18.10

Một vật có khối lượng 15 kg đang đứng yên thì bắt đầu chuyển động nhanh dần đều, sau khi đi được 150 m vật đạt vận tốc 54 km/h. Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,05. Lấy g = 9,8 m/s². Xác định lực kéo tác dụng vào vật theo phương song song với phương chuyển động.

Phương pháp giải:

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn chiều dương là chiều chuyển động của vật. Chiếu phương trình lên chiều dương, ta được: F_k – F_mst = ma => F_k = F_mst + ma

Mà F_mst = μN = μP = μmg.

Áp dụng công thức độc lập thời gian để tính a: v² – v₀² = 2as => a = \(\frac{{{v^2} - v_0^2}}{{2s}}\)

Lời giải chi tiết:

Theo định luật II Newton ta có: \(\overrightarrow {{F_k}}  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn chiều dương là chiều chuyển động của vật. Chiếu phương trình lên chiều dương, ta được: F_k – F_mst = ma => F_k = ma + F_mst

Mà F_mst = μN = μP = μmg.

Áp dụng công thức độc lập thời gian: v² – v₀² = 2as => a = \(\frac{{{v^2} - v_0^2}}{{2s}}\) = \(\frac{{{v^2}}}{{2s}}\)(v₀ = 0).

=> F = ma + μmg = m\(\frac{{{v^2}}}{{2s}}\)+ μmg = \(\frac{{{{15.15}^2}}}{{2.150}}\)+ 0,05.15.9,8 = 18,6 N.

Vậy lực kéo tác dụng vào vật theo phương song song với phương chuyển động co độ lớn là 18,6 N.

18.11

Một vật có khối lượng 2 000 g được đặt trên một bàn dài nằm ngang. Tác dụng lên vật một lực có độ lớn 5N theo phương song song với mặt bàn trong khoảng thời gian 2 s rồi thôi tác dụng lực. Biết hệ số ma sát giữa vật và mặt bàn là 0,2. Lấy g = 10 m/s. Tính quãng đường tổng cộng mà vật đi được cho đến khi dừng lại.

Phương pháp giải:

Theo định luật II Newton:

Khi tác dụng lực, ta có: \(\overrightarrow F  + \overrightarrow {{F_{mst}}}  = m\overrightarrow {{a_1}} \)

Khi ngừng tác dụng lực, ta có: \(\overrightarrow {{F_{mst}}}  = m\overrightarrow {{a_2}} \)

Tìm a trong từng trường hợp, sau đó tính quãng đường vật đi được trong từng trường hợp bằng công thức: s₁ = v₀t + \(\frac{1}{2}a{t^2}\)và v² – v₁² = 2a₂s₂.

Tổng cộng quãng đường mà vật đi được: s =s₁ + s₂.

Lời giải chi tiết:

Đổi m = 2000 g = 2 kg. Chọn chiều (+) là chiều chuyển động của vật.

Theo định luật II Newton:

Khi tác dụng lực, ta có: \(\overrightarrow F  + \overrightarrow {{F_{mst}}}  = m\overrightarrow {{a_1}} \)

Chiếu lên chiều (+), ta được: F – F_mst = ma₁ => F = ma₁ + F_mst

Mà F_mst = μN = μP = μmg.

=> F = ma₁ + μmg => a₁ = \(\frac{{F - \mu mg}}{m}\)=\(\frac{{5 - 0,2.2.10}}{2}\)= 0,5 m/s².

Quãng đường vật đi được trong 2 giây đầu:

s₁ = v₀t + \(\frac{1}{2}{a_1}{t^2}\)=\(\frac{1}{2}{a_1}t\) = \(\frac{1}{2}\).0,5.2² = 1m.

Sau 2 giây, vật chuyển động chậm dần dưới tác dụng của lực ma sát: \(\overrightarrow {{F_{mst}}}  = m\overrightarrow {{a_2}} \)

Chiếu lên chiều (+), ta có: -F_ms = ma₂ => a₂ = -μg = - 2 m/s².

Quãng đường đi được từ lúc ngừng lực tác dụng tới khi dừng hẳn:

Áp dụng công thức độc lập thời gian: v² – v₁² = 2a₂s₂

=> s₂ = \(\frac{{{v^2} - {v_1}^2}}{{2{a_2}}}\)= \(\frac{{ - {{({v_0} + {a_1}t)}^2}}}{{2{a_2}}}\)= \(\frac{{ - {{(0,5.2)}^2}}}{{2( - 2)}}\)= 0,25m.

=> Tổng quãng đường: s = s₁ + s₂ = 1,25 m.

18.12

Một khúc gỗ khối lượng 2,5 kg đặt trên sàn nhà. Người ta kéo khúc gỗ bằng một lực \(\overrightarrow F \) hướng chếch lên và hợp với phương nằm ngang một góc α = 30°. Khúc gỗ chuyển động nhanh dần đều với gia tốc 1,5 m/s² trên sàn. Biết hệ số ma sát trượt giữa gỗ và sàn là 0,25. Lấy g = 10 m/s². Tính độ lớn của lực \(\overrightarrow F \).

Phương pháp giải:

Theo định luật II Newton ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn hệ trục Oxy có chiều dương hướng lên (Oy), từ trái sang phải (Ox). Chiếu phương trình lần lượt lên trục Ox, Oy. Giải hệ phương trình.

Lời giải chi tiết:

Theo định luật II Newton ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{mst}}}  = m\overrightarrow a \).

Chọn hệ trục Oxy có chiều dương hướng lên (Oy), từ trái sang phải (Ox) như hình vẽ. Chiếu phương trình lần lượt lên trục Ox, Oy. Ta được:

Chiếu xuống Ox, ta có:

Fcosα – F_mst = ma => F_mst = Fcosα - ma                          

Chiếu xuống Oy, ta có:

Fsinα – P + N = 0 => N = P - Fsinα   

Mặt khác, ta có: F_mst = μN

=> Fcosα - ma = μ(P – Fsinα) ó F(cosα + μsinα) = μP + ma.

=> F = \(\frac{{ma + \mu P}}{{\cos \alpha  + \mu \sin \alpha }}\)= \(\frac{{2,5.1,5 + 0,25.2,5.10}}{{\cos {{30}^o} + 0,25\sin {{30}^o}}}\) ≈ 10,1 N.