Bài 7. Đồ thị độ dịch chuyển - thời gian trang 10, 11, 12 SBT Vật lí 10 Kết nối tri thức với cuộc sốngDựa vào đồ thị độ dịch chuyển - thời gian của một chuyển động thẳng đều có thể xác định được vận tốc của chuyển động bằng công thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
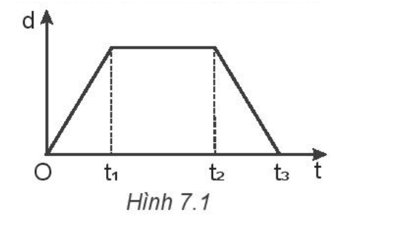
7.1 Dựa vào đồ thị độ dịch chuyển - thời gian của một chuyển động thẳng đều có thể xác định được vận tốc của chuyển động bằng công thức A. \(v = \frac{{{d_1} + {d_2}}}{{{t_1} + {t_2}}}\) B. \(v = \frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\) C. \(v = \frac{{{d_1} + {d_2}}}{{{t_2} - {t_1}}}\) D. \(v = \frac{{{d_2} - {d_1}}}{{{t_1} - {t_2}}}\) Phương pháp giải: Sử dụng công thức d = vt. Lời giải chi tiết: Từ đồ thị ta có d = d2 – d1; t = t2 – t1 Ta có công thức d = vt => d2 – d1 = v(t2 – t1) ⇨ \(v = \frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\) Chọn đáp án B. 7.2 Theo đồ thị ở Hình 7.1, vật chuyển động thẳng đều trong khoảng thời gian
A. từ 0 đến \({t_2}\). B. từ \({t_1}\) đến \({t_2}\) . C. từ 0 đến \({t_1}\) và từ \({t_2}\) đến \({t_3}\). D. từ 0 đến \({t_3}\). Phương pháp giải: Vận dụng kiến thức về chuyển động thẳng đều. Lời giải chi tiết: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng có tốc độ trung bình như nhau tại mỗi quãng đường. Trong chuyển động thẳng đều quãng đường đi được s tỉ lệ thuận với thời gian chuyển động t. Qua đồ thị ta thấy vật chuyển động thẳng đều trong khoảng thời gian từ 0 đến \({t_1}\) và từ \({t_2}\) đến \({t_3}\). Trong khoảng thời gian từ t1 – t2 vật đứng yên không chuyển động. Chọn đáp án C. 7.3 Cặp đồ thị nào ở hình dưới đây là của chuyển động thẳng đều?
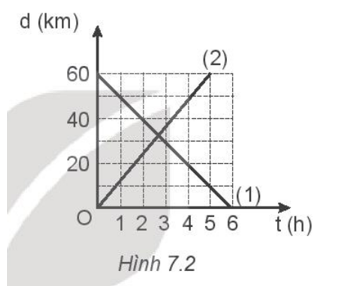
Phương pháp giải: Vận dụng kiến thức về chuyển động thẳng đều. Lời giải chi tiết: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng có tốc độ trung bình như nhau tại mỗi quãng đường. Trong chuyển động thẳng đều quãng đường đi được s tỉ lệ thuận với thời gian chuyển động t. (I) là đồ thị của chuyển động thẳng đều (độ dịch chuyển tỉ lệ thuận với thời gian chuyển động). (II) là đồ thị của vật đứng yên (độ dịch chuyển không đổi theo thời gian chuyển động). (III) là đồ thị của chuyển động biến đổi đều (vận tốc tỉ lệ thuận với thời gian chuyển động). (IV) là đồ thị của chuyển động thẳng đều (vận tốc không đổi theo thời gian chuyển động). Chọn đáp án B. 7.4 Phương trình chuyển động và độ lớn vận tốc của hai chuyển động có đồ thị ở Hình 7.2 là:
A. \(\begin{array}{l}{d_1} = 60 - 10t;{v_1} = 10km/h\\{d_2} = 12t;{v_2} = 12km/h\end{array}\) B. \(\begin{array}{l}{d_1} = 60 + 10t;{v_1} = 10km/h\\{d_2} = - 10t;{v_2} = 10km/h\end{array}\) C. \(\begin{array}{l}{d_1} = 60 - 20t;{v_1} = 20km/h\\{d_2} = 12t;{v_2} = 12km/h\end{array}\) D. \(\begin{array}{l}{d_1} = - 10t;{v_1} = 10km/h\\{d_2} = 12t;{v_2} = 12km/h\end{array}\) Phương pháp giải: - Sử dụng cách đọc số liệu từ đồ thị: xác định do và d tại một thời điểm t bất kì. - Sử dụng công thức tính độ dịch chuyển và vận tốc của chuyển động thẳng đều: d = d0 + vt; v = \(\frac{{\Delta d}}{{\Delta t}}\) Lời giải chi tiết: Căn cứ vào đồ thị Hình 7.2 ta có thể xác định được: - Chuyển động (1) có: Độ dịch chuyển ban đầu: d0 = 60 km Độ dịch chuyển tại t = 6 h là d = 0 km Vận tốc của chuyển động là: v = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{d - {d_0}}}{{t - {t_0}}}\)= \(\frac{{0 - 60}}{{6 - 0}}\)= \(\frac{{ - 60}}{6}\)= -10 km/h Phương trình chuyển động: d1 = do + vt = 60 – 10t. Độ lớn vận tốc của chuyển động: ϑ1 = 10 km/h. - Chuyển động (2) có: Độ dịch chuyển ban đầu: d0 = 0 km Độ dịch chuyển tại t = 5 h là d = 60 km Vận tốc của chuyển động là: v = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{d - {d_0}}}{{t - {t_0}}}\)= \(\frac{{60 - 0}}{{5 - 0}}\)= \(\frac{{60}}{5}\)= 12 km/h Phương trình chuyển động: d2 = do + vt = 12t. Độ lớn vận tốc của chuyển động: ϑ2 = 12 km/h. Chọn đáp án A. 7.5 Dựa vào đồ thị ở Hình 7.3, xác định:
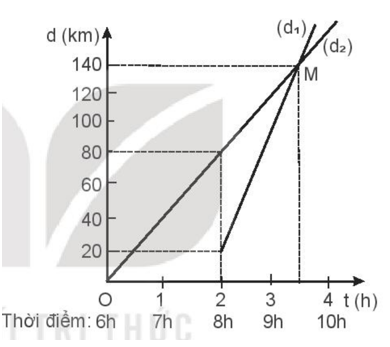
a) Vận tốc của mỗi chuyển động. b) Phương trình của mỗi chuyển động. c) Vị trí và thời điểm các chuyển động gặp nhau. Phương pháp giải: Sử dụng cách đọc số liệu từ đồ thị xác định d0 và d tại một thời điểm t bất kì. Sử dụng công thức tính vận tốc và phương trình của chuyển động thẳng đều: v = \(\frac{{\Delta d}}{{\Delta t}}\); d = d0 + vt Để xác định vị trí và thời gian các chuyển động gặp nhau ta cho phương trình của các chuyển động bằng nhau. Lời giải chi tiết: a) Chuyển động (I): Tại thời điểm t0 = 0, d0 = 0 km; Tại thời điểm t1 = 3 h, d1 = 180 km; Ta có vận tốc của chuyển động (I) là: v1 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{180 - 0}}{{3 - 0}}\)= \(\frac{{180}}{3}\)= 60 km/h Chuyển động (II): Tại thời điểm t0 = 0, d0 = 180 km; Tại thời điểm t1 = 3 h, d1 = 0 km; Ta có vận tốc của chuyển động (II) là: v2 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{0 - 180}}{{3 - 0}}\)= \(\frac{{ - 180}}{3}\)= -60 km/h Chuyển động (III): Tại thời điểm t0 = 0, d0 = 0 km; Tại thời điểm t1 = 3 h, d1 = 60 km; Ta có vận tốc của chuyển động (II) là: v3 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{60 - 0}}{{3 - 0}}\)= \(\frac{{60}}{3}\)= 20 km/h b) Phương trình chuyển động có dạng: d = do + vt. Phương trình chuyển động (I) có dạng: d1 = do1 + v1t = 0 + 60t = 60t (km). Phương trình chuyển động (II) có dạng: d2 = do2 + v1t = 180 – 60t (km). Phương trình chuyển động (III) có dạng: d3 = do3 + v1t = 0 + 20t = 20t (km). c) Chuyển động (I) gặp (II) khi d1 = d2 \( \Leftrightarrow \) 60t = 180 – 60t \( \Leftrightarrow \) t = 1,5 h => d1 = 90 km Chuyển động (II) gặp (III) khi d2 = d3 \( \Leftrightarrow \) 180 - 60t = 20t \( \Leftrightarrow \) t = 2,25 h => d1 = 45 km Vậy (I) và (II) gặp nhau tại thời điểm 1,5h, cách điểm khởi hành của (I) 90 km. (II) và (III) gặp nhau tại thời điểm 2,25h, cách điểm khởi hành của (II) 45 km. 7.6 Một xe máy xuất phát từ A lúc 6 giờ chạy thẳng tới B với vận tốc không đổi 40 km/h. Một ô tô xuất phát từ B lúc 8 giờ chạy với vận tốc không đổi 80 km/h theo cùng hướng với xe máy. Biết khoảng cách AB = 20 km. Chọn thời điểm 6 giờ là mốc thời gian, chiều từ A đến B là chiều dương. Xác định vị trí và thời điểm ô tô đuổi kịp xe máy bằng công thức và bằng đồ thị. Phương pháp giải: Vẽ đồ thị. Viết phương trình của chuyển động theo CT: d = d0 + vt Cho phương trình của các chuyển động bằng nhau, giải pt. Lời giải chi tiết:
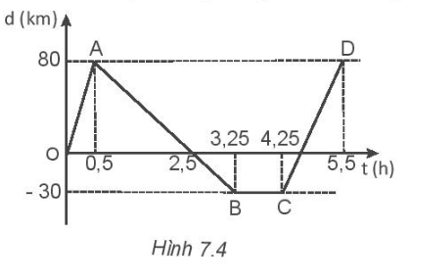
Ta có các phương trình chuyển động: Xe máy: d1 = d01 + v1t = 40t. Ô tô: d2 = d02 + v2t = 20 + 80t. Từ đồ thị ta thấy ô tô và xe máy gặp nhau tại điểm M có dM = 140 km và tM = 3,5h. Khi hai xe gặp nhau thì ta có d1 = d2 ⇨ 40t = 80t – 140 ⇨ t = 3,5h ⇨ d1 = d2 = 140 Vậy thời điểm hai xe gặp nhau là: 3,5 h + 6h = 9,5h. Địa điểm gặp nhau cách điểm khởi hành của xe máy d1 = 140 km. 7.7 Đồ thị độ dịch chuyển – thời gian của một chuyển động thẳng được vẽ trong Hình 7.4.
a) Hãy mô tả chuyển động. b) Xác định tốc độ và vận tốc của chuyển động trong các khoảng thời gian: - Từ 0 đến 0,5 giờ. - Từ 0,5 đến 2,5 giờ. - Từ 0 đến 3,25 giờ. - Từ 0 đến 5,5 giờ. Phương pháp giải: Quan sát đồ thị để mô tả chuyển động Sử dụng công thức tính vận tốc và tốc độ của chuyển động v = \(\frac{{\Delta d}}{{\Delta t}}\); ϑ = \(\frac{s}{{\Delta t}}\) Lời giải chi tiết: a) Trong khoảng thời gian từ 0 đến 0,5 h, từ 0,5h đến 3,25 h và từ 4,25 h đến 5,5 h vật chuyển động thẳng đều. Trong khoảng thời gian từ 3,25 h đến 4,25 h vật đứng yên không chuyển động. b) - Trong khoảng thời gian từ 0 đến 0,5 giờ: vật chuyển động thẳng đều nên vận tốc bằng tốc độ chuyển động: v = ϑ = \(\frac{{80}}{{0,5}} = 160\)km. - Trong khoảng thời gian từ 0,5 đến 2,5 giờ: v = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)=\(\frac{{0 - 80}}{{2,5 - 0,5}}\)=\(\frac{{ - 80}}{2}\)= -40 km/h ϑ = \(\frac{s}{{\Delta t}}\) = \(\frac{{80}}{2}\)= 40 km/h Trong khoảng thời gian từ 0 đến 3,25 giờ: v = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_3} - {d_1}}}{{{t_3} - {t_1}}}\)= \(\frac{{ - 30 - 0}}{{3,25 - 0}}\)= \(\frac{{ - 30}}{{3,25}}\)≈ -9,2 km/h. ϑ = \(\frac{s}{{\Delta t}}\)= \(\frac{{80 + 80 + 30}}{{3,25}}\)≈58 km/h. Trong khoảng thời gian từ 0 đến 5,5 giờ: v = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_4} - {d_1}}}{{{t_4} - {t_1}}}\)= \(\frac{{80 - 0}}{{5,5 - 0}}\)= \(\frac{{80}}{{5,5}}\)≈ 14,5 km/h. ϑ = \(\frac{s}{{\Delta t}}\)= \(\frac{{80 + 80 + 30 + 30 + 80}}{{5,5}}\)≈ 54,5 km/h. 7.8 Hình 7.5 vẽ đồ thị chuyển động của ba vật.
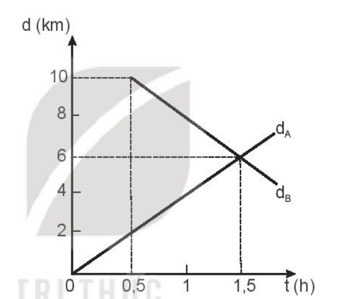
a) Vật nào chuyển động thẳng đều, vật nào chuyển động không đều? b) Tính vận tốc của vật (1) và (II). c) Lập phương trình chuyển động của vật (1) và (II). d) Xác định vị trí và thời điểm vật (1) gặp vật (II). Phương pháp giải: Dựa vào đồ thị để xác định vật chuyển động thẳng đều. Sử dụng công thức tính vận tốc: v = \(\frac{{\Delta d}}{{\Delta t}}\). Viết phương trình chuyển động của vật theo công thức: d = d0 + vt Cho phương trình chuyển động của 2 vật bằng nhau. Giải phương trình. Từ đó tìm ra vị trí và thời điểm gặp nhau của 2 vật. Lời giải chi tiết: a) (I) và (II) chuyển động thẳng đều vì có đồ thị dịch chuyển – thời gian là đường thẳng. (III) là chuyển động thẳng không đều vì đồ thị độ dịch chuyển thời gian là đường cong. b) vI = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)=\(\frac{{40 - 0}}{{4 - 0}}\)=\(\frac{{40}}{4}\)=10 m/s. vII = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)=\(\frac{{0 - 40}}{{8 - 0}}\)=\(\frac{{ - 40}}{8}\)= -5 m/s. c) Phương trình chuyển động được xác định theo công thức: d = d0 + vt dI = d0I + vIt = 10t (m) dII = d0II + vIIt = 40 – 5t (m) d) (I) và (II) gặp nhau tại điểm M khi: dI = dII \( \Leftrightarrow \) 10t = 40 – 5t \( \Leftrightarrow \) t ≈ 2,67 s => dI ≈ 26,7 m Vậy vật (I) và (II) gặp nhau sau 2,67 s tại vị trí cách điểm khởi hành của vật (I) 26,7 m. 7.9 Hai người ở hai đầu một đoạn đường thẳng AB dài 10km đi bộ đến gặp nhau. Người ở A đi trước người ở B 0,5h. Sau khi người ở B đi được 1h thì hai người gặp nhau. Biết hai người đi nhanh như nhau. a) Tính vận tốc của hai người. b) Viết phương trình chuyển động của hai người. c) Vẽ đồ thị độ dịch chuyển – thời gian cho chuyển động của hai người trên cùng một hệ trục toạ độ. d) Xác định vị trí và thời điểm hai người gặp nhau. Phương pháp giải: Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc người ở A xuất phát. Tính độ lớn vận tốc của mỗi người theo CT: v = \(\frac{s}{t}\) Viết phương trình chuyển động theo CT: d = d0 + vt Cho phương trình chuyển động của 2 người bằng nhau. Giải phương trình. Từ đó tìm ra vị trí và thời điểm gặp nhau. Lời giải chi tiết: Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc người ở A xuất phát. Vì 2 người đi nhanh như nhau nên vận tốc chuyển động của 2 người có độ lớn bằng nhau: |v1| = |v2| = v Mà khi 2 người gặp nhau thì người xuất phát từ B đi được 1h. ⇨ Người xuất phát từ A đi được 1,5 h. Ta có: quãng đường người A đi được là: sA = vAtA = 1,5v. Quãng đường người B đi được là: sB = vBtB = 1v Khi đó ta có AB = sA + sB = 1,5v + v = 10 => v = 4 km/h. a) Vì chọn chiều dương từ A đến B nên vận tốc của người xuất phát từ A là vA = 4 km/h, vận tốc của người xuất phát từ B là vB = -4 km/h. b) Phương trình chuyển động của người xuất phát từ A: dA = d0A + vAt = 4t (km) Phương trình chuyển động của người xuất phát từ B: dB = d0B + vBt = 10 – 4(t – 0,5) (km) c) Đồ thị:
d) Hai người gặp nhau khi dA = dB \( \Leftrightarrow \) 4t = 10 – 4(t – 0,5) \( \Leftrightarrow \) t = 1,5 h ⇨ dA = 6 km Vậy hai người gặp nhau sau khi người A xuất phát từ A và đi được 1,5 h tại vị trí cách A một khoảng 6 km.
|























Danh sách bình luận