Bài 13. Tổng hợp và phân tích lực trang 25, 26, 27 SBT Vật lí 10 Kết nối tri thức với cuộc sống

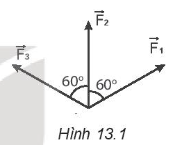
13.1

Một chất điểm chịu tác dụng đồng thời của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) thì hợp lực \(\overrightarrow F \) của chúng luôn có độ lớn thoả mãn hệ thức

A. F = F₁ – F₂.                                     B. F = F₁ + F₂.

C. | F₁ – F₂ | ≤ F ≤ F₁ + F₂.                  D. F₂ = F₁² + F₂².

Phương pháp giải:

Vận dụng biểu thức vectơ lực tổng hợp sau: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Lời giải chi tiết:

Ta có vectơ lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \).

Độ lớn lực tổng hợp: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \).

Khi đó ta có các trường hợp đặc biệt sau:

+ \(\overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_2}} \) => F = F₁ + F₂
+ \(\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_2}} \) => F = | F₁ - F₂ |
+ \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_2}} \) => \(F = \sqrt {F_1^2 + F_2^2} \)

 => | F₁ - F₂ | ≤ F ≤ F₁ + F₂

Chọn đáp án C.

13.2

Hợp lực của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) hợp với nhau một góc α có độ lớn thoả mãn hệ thức

A. F = F1 + F2.                                  B. F = F₁ – F₂.      

C. F² = F₁² + F₂² – 2F₁F₂cosα.            D. F² = F₁² + F₂² + 2F₁F₂cosα.

Phương pháp giải:

Vận dụng biểu thức vectơ lực tổng hợp sau: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Lời giải chi tiết:

Ta có vectơ lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \).

Độ lớn lực tổng hợp: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\alpha } \)

=> F² = F₁² + F₂² + 2F₁F₂cosα

Chọn đáp án D.

13.3

Nếu một chất điểm chuyển động dưới tác dụng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) khác phương, \(\overrightarrow F \) là hợp lực của hai lực đó thì vectơ gia tốc của chất điểm

A. cùng phương, cùng chiều với lực \(\overrightarrow {{F_1}} \).

B, cùng phương, cùng chiều với lực \(\overrightarrow {{F_2}} \).

C. cùng phương, cùng chiều với lực \(\overrightarrow F \).

D. cùng phương, ngược chiều với lực \(\overrightarrow F \).

Phương pháp giải:

Vận dụng lý thuyết về tổng hợp lực.

Lời giải chi tiết:

Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy. Lực thay thế này gọi là hợp lực.

Trong câu này\(\overrightarrow F \) là hợp lực của hai lực\(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) khác phương nên vectơ gia tốc của chất điểm sẽ cùng phương, cùng chiều với lực \(\overrightarrow F \).

Chọn đáp án C.

13.4

Một chất điểm chịu tác dụng của một lực \(\overrightarrow F \) có độ lớn là 20 N. Nếu hai lực thành phần của lực đó vuông góc với nhau có độ lớn lần lượt là F₁ = 12 N và F₂ thì F₂ bằng

A. 8N.         B. 16 N.      C. 32 N       D. 20 N.

Phương pháp giải:

Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp hai lực thành phần vuông góc: \(F = \sqrt {F_1^2 + F_2^2} \)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_2}} \) => \(F = \sqrt {F_1^2 + F_2^2} \)

=> F² = F₁² + F₂² = => F₂ = \(\sqrt {{F^2} - F_1^2} \)= \(\sqrt {{{20}^2} - {{12}^2}} \)= 16 N.

Chọn đáp án B.

13.5

Hai lực có giá đồng quy có độ lớn là 6 N và 8 N và có phương vuông góc với nhau. Hợp lực của hai lực này có độ lớn là

A. 4N.         B. 10 N.      C. 2 N.        D.48 N

Phương pháp giải:

Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp hai lực thành phần vuông góc: \(F = \sqrt {F_1^2 + F_2^2} \)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_2}} \) => \(F = \sqrt {F_1^2 + F_2^2} \)=\(\sqrt {{6^2} + {8^2}} \)= 10N.

Chọn đáp án B.

13.6

Hai lực khác phương \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có độ lớn F₁ = F₂ = 20 N, góc tạo bởi hai lực này là 60°. Hợp lực của hai lực này có độ lớn là

A. 14,1 N.    B. \(20\sqrt 3 \) N.    C. 17,3 N.    D. 20 N.

Phương pháp giải:

Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp tổng quát:

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \)

(φ: góc hợp giữa hai lực thành phần)

Lời giải chi tiết:

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \)= \(\sqrt {{{20}^2} + {{20}^2} + 2.20.20.\cos {{60}^o}} \)= 20\(\sqrt 3 \)N.

Chọn đáp án B.

13.7

Hai lực khác phương có độ lớn bằng 9 N và 12 N. Hợp lực của hai lực này không thể có độ lớn nào sau đây?

A. 2 N.        B. 15 N.       C. 11,1 N.     D. 21 N.

Phương pháp giải:

Sử dụng công thức: |F1 – F2| ≤ F ≤ F1 + F2

Lời giải chi tiết:

Ta luôn có: |F1 – F2| ≤ F ≤ F1 + F2 => 3 N ≤ F ≤ 21 N.

=> Hợp lực của hai lực này không thể có độ lớn là 2 N.

 Chọn đáp án A.

13.8

Một chất điểm chịu tác dụng của hai lực có độ lớn 18 N và 24 N. Biết hợp lực của hai lực này có giá trị 30 N, góc tạo bởi hai lực này là

A. 90^o.         B. 30°.        C. 45°.        D. 60°.

Phương pháp giải:

Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp tổng quát:

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \)

Lời giải chi tiết:

Ta có độ lớn của lực tổng hợp được tính bằng công thức: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \)

=> cosφ = \(\frac{{{F^2} - F_1^2 - F_2^2}}{{2{F_1}{F_2}}}\)= \(\frac{{{{30}^2} - {{24}^2} - {{18}^2}}}{{2.24.18}}\)= 0 => φ = 90^o.

Chọn đáp án A.

13.9

Một chất điểm chịu tác dụng của ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có cùng độ lớn 12 N. Biết góc tạo bởi các lực \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = (\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ) = {60^o}\) (Hình 13.1). Hợp lực của ba lực này có độ lớn là

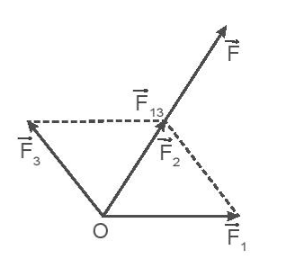
A. 6 N.        B. 24 N.       C. 10,4 N.             D. 20,8 N.

Phương pháp giải:

Vectơ lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_2}} \)

Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp tổng quát:

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \).

Lời giải chi tiết:

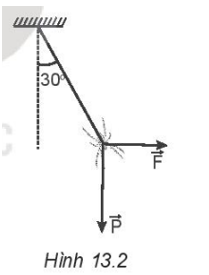
Hợp lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_2}} \)

Theo quy tắc hình bình hành và kết hợp với điều kiện ba lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \)có độ lớn bằng nhau => Hình bình hành thành hình thoi nên hợp lực của \(\overrightarrow {{F_1}} \)và \(\overrightarrow {{F_3}} \)cùng phương, cùng chiều với lực \(\overrightarrow {{F_2}} \)nên độ lớn hợp lực của ba lực trên là:

F = F₁₃ + F₂ hay F = \(\sqrt {F_1^2 + F_3^2 + 2{F_1}{F_3}\cos {{120}^o}}  + {F_2}\)= 24 N.

Chọn đáp án B.

13.10

Một con nhện đang treo mình dưới một sợi tơ theo phương thẳng đứng thì bị một cơn gió thổi theo phương ngang làm dây treo lệch đi so với phương thẳng đứng một góc 30°. Biết trọng lượng của con nhện là P = 0,1 N. Xác định độ lớn của lực mà gió tác dụng lên con nhện ở vị trí cân bằng trong Hình 13.2.

Phương pháp giải:

Viết phương trình cân bằng lực: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow T  = \overrightarrow 0 \)

Tổng hợp lực theo quy tắc hình bình hành.

Lời giải chi tiết:

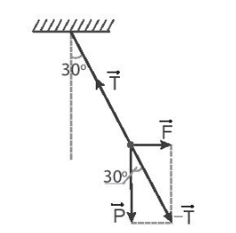
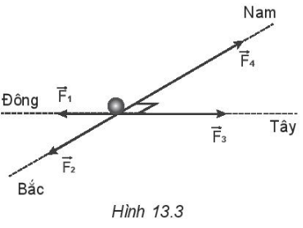
Khi con nhện và sợi tơ cân bằng như hình vẽ:

Ta có: tan30^o = \(\frac{F}{P}\)

=> F = Ptan30^o = \(\frac{{0,1}}{{\sqrt 3 }}\)≈ 0,058 N.

13.11

Một vật chịu tác dụng đồng thời của bồn lực như Hình 13.3. Độ lớn của các lực lần lượt là F₁ = 10 N, F₂ = 20 N, F₃ = 22 N, F₄ = 36 N. Xác định phương, chiều và độ lớn của hợp lực do các lực này tác dụng lên vật.

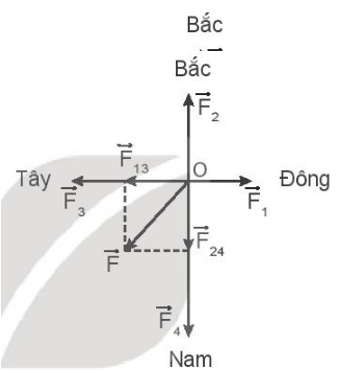
Phương pháp giải:

Vectơ lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}} \).

Tổng hợp lần lượt các lực để xác định được hợp lực của cả 4 lực này.

Vì \(\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}} \)=> F₁₃ = |F₁ – F₃|

Và \(\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_4}} \)=> F₂₄ = |F₂ – F₄|

Khi đó ta có thể thấy \(\overrightarrow {{F_{13}}}  \bot \overrightarrow {{F_{24}}} \) => F = \(\sqrt {F_{13}^2 + F_{24}^2} \)

Lời giải chi tiết:

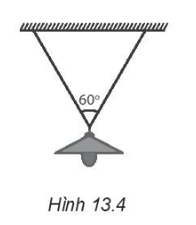
Hợp lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}} \).

Vì \(\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}} \)=> F₁₃ = |F₁ – F₃| = 12 N

F₁ < F₃ => F₁₃ cùng phương F₃ và có chiều từ Đông sang Tây.

Và \(\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_4}} \)=> F₂₄ = |F₂ – F₄| = 16 N

F₂ < F₄ => F₂₄ cùng phương F4và có chiều từ Bắc sang Nam.

Khi đó ta có thể thấy: \(\overrightarrow {{F_{13}}}  \bot \overrightarrow {{F_{24}}} \)

Độ lớn hợp lực là:

F = \(\sqrt {F_{13}^2 + F_{24}^2} \)= \(\sqrt {{{12}^2} + {{16}^2}} \)= 20 N.

Vậy hợp lực F có phương và chiều như hình vẽ, độ lớn F = 20 N.

13.12

Một cái đèn được treo vào hai sợi dây giống nhau như Hình 13.4. Biết trọng lượng của đèn là 25 N, hai dây làm thành góc 60°. Xác định lực căng của dây.

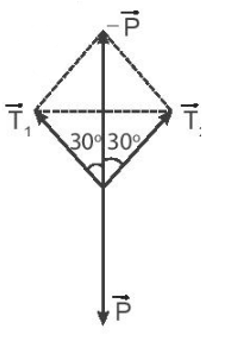
Phương pháp giải:

Viết phương trình cân bằng lực: \(\overrightarrow {{T_1}}  + \overrightarrow {{T_2}}  + \overrightarrow P  = \overrightarrow 0 \)

Lời giải chi tiết:

Khi đèn và dây treo cân bằng, các lực tác dụng lên đèn được biểu diễn như hình vẽ.

Theo hình vẽ ta có phương trình cân bằng lực:

\(\overrightarrow {{T_1}}  + \overrightarrow {{T_2}}  + \overrightarrow P  = \overrightarrow 0 \) => \(\overrightarrow {{T_1}}  + \overrightarrow {{T_2}}  =  - \overrightarrow P \)

Mà về độ lớn: T₁ = T₂ = T=> P = \(2T\cos {30^o}\)

T = \(\frac{P}{{\sqrt 3 }}\)=\(\frac{{25}}{{\sqrt 3 }}\)≈ 14,4 N.

Vậy lực căng dây T có cùng phương, ngược chiều với P như hình vẽ và có độ lớn T ≈ 14,4 N.