Phần câu hỏi bài 1 trang 5 Vở bài tập toán 8 tập 2Giải phần câu hỏi bài 1 trang 5 VBT toán 8 tập 2. Cho hai phương trình (1) và (2) tương đương với nhau ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1. Cho hai phương trình (1) và (2) tương đương với nhau. Biết rằng phương trình (1) có tập nghiệm \(S = {\rm{\{ }} - 3;2\} .\) Khi đó một nghiệm của phương trình (2) là: (A) \(-2\); (B) \(3\); (C) \(-3\); (D) \(-1\). Khoanh tròn vào chữ cái trước khẳng định đúng. Phương pháp giải: Sử dụng: Hai phương trình tương đương là hai phương trình (cùng ẩn) có cùng tập nghiệm. Lời giải chi tiết: Hai phương trình (1) và (2) tương đương với nhau nên phương trình (2) cũng có tập nghiệm là \(S = {\rm{\{ }} - 3;2\} .\) Chọn C. Câu 2. Số \(x=-1\) không phải là nghiệm của phương trình nào trong các phương trình sau đây? (A) \(-|x|+1=0;\) (B) \(-|-x|+1=0;\) (C) \((-x)^2-1=0;\) (D) \(-x^2-1=0.\) Khoanh tròn vào chữ cái trước khẳng định đúng. Phương pháp giải: Lần lượt thay \(x=-1\) vào các phương trình đã cho, nếu \(x\) không thỏa mãn phương trình nào thì nó không là nghiệm của phương trình đó. Lời giải chi tiết: - Thay \(x=-1\) vào phương trình \(-|x|+1=0\) ta được: \( - | - 1| + 1 = 0\) Vậy \(x=-1\) là nghiệm của phương trình \(-|x|+1=0\). - Thay \(x=-1\) vào phương trình \(-|-x|+1=0\) ta được: \( - \left| { - \left( { - 1} \right)} \right| + 1 = 0\) Vậy \(x=-1\) là nghiệm của phương trình \(-|-x|+1=0\). - Thay \(x=-1\) vào phương trình \((-x)^2-1=0\) ta được: \({\left[ { - \left( { - 1} \right)} \right]^2} - 1 = 0\) Vậy \(x=-1\) là nghiệm của phương trình \((-x)^2-1=0\). - Thay \(x=-1\) vào phương trình \(-x^2-1=0\) ta được: \(- {\left( { - 1} \right)^2} - 1 = - 2 \ne 0\) Vậy \(x=-1\) không là nghiệm của phương trình \(-x^2-1=0\). Chọn D. Câu 3. Hãy nối mỗi phương trình ở cột trái với số là nghiệm của nó ở cột phải:
Phương pháp giải: Lần lượt thay \(x=2;-2;5\) vào các phương trình (a), (b), nếu giá trị nào của \(x\) thỏa mãn phương trình thì giá trị đó là nghiệm của phương trình. Lời giải chi tiết: - Thay \(x=2\) vào phương trình (a) ta được: \(2.2 - 1 \ne \dfrac{{3.2 + 1}}{2} + 1\) Vậy \(x=2\) không là nghiệm của phương trình (a). - Thay \(x=-2\) vào phương trình (a) ta được: \(2.\left( { - 2} \right) - 1 \ne \dfrac{{3.\left( { - 2} \right) + 1}}{2} + 1\) Vậy \(x=-2\) không là nghiệm của phương trình (a). - Thay \(x=5\) vào phương trình (a) ta được: \(2.5 - 1 = \dfrac{{3.5 + 1}}{2} + 1\) \((=9)\) Vậy \(x=5\) là nghiệm của phương trình (a). - Thay \(x=2\) vào phương trình (b) ta được: \({2^2} + 2 + 1 \ne 7 + 2.2\) Vậy \(x=2\) không là nghiệm của phương trình (b). - Thay \(x=-2\) vào phương trình (b) ta được: \({\left( { - 2} \right)^2} + \left( { - 2} \right) + 1 = 7 + 2.\left( { - 2} \right)\) Vậy \(x=-2\) là nghiệm của phương trình (b). - Thay \(x=5\) vào phương trình (b) ta được: \({5^2} + 5 + 1 \ne 7 + 2.5\) Vậy \(x=5\) không là nghiệm của phương trình (b). Ta nối như sau:
Loigiaihay.com
|















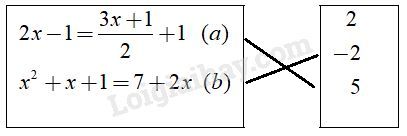






Danh sách bình luận