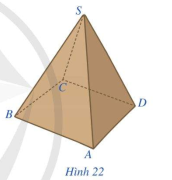
Giải mục 4 trang 91, 92, 93 SGK Toán 11 tập 1 - Cánh Diều

Hoạt động 8

Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:

a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?

b) Mỗi mặt của hộp quà lưu niệm có dạng hình gì?

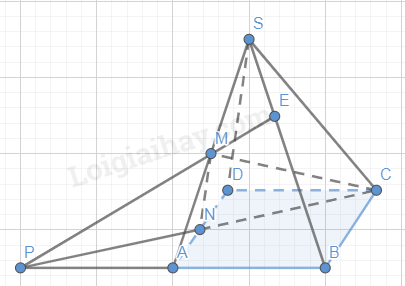
Phương pháp giải:

Trong mặt phẳng (P), cho đa giác\({A_1}{A_2}...{A_n}\) .Lấy điểm S nằm ngoài (P). Nối S với các đỉnh\({A_1},{A_2},...,{A_n}\)ta được n tam giác:\(S{A_1}{A_2},S{A_{_2}}{A_3},...,S{A_n}{A_1}\).Hình gồm đa giác\({A_1}{A_2}...{A_n}\) và n tam giác\(S{A_1}{A_2},S{A_{_2}}{A_3},...,S{A_n}{A_1}\)gọi là hình chóp

Lời giải chi tiết:

a) Đỉnh S không nằm trong mặt phẳng (ABCD).

b) Một mặt của hộp quà lưu niệm có dạng hình tam giác.

Luyện tập 5

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.

a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB

b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC)

Phương pháp giải:

Để xác định giao điểm của mặt phẳng với các đường thẳng, ta tìm điểm chung giữa mặt phẳng và các đường thẳng đó

Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung giữa hai mặt phẳng. Đoạn thẳng nối hai điểm chung đó là giao tuyến giữa hai mặt phẳng.

Lời giải chi tiết:

a) Gọi P là giao điểm của CN và AB

Ta có \(P \in CN\)suy ra \(P \in (CMN)\)

Suy ra P là giao điểm của mặt phẳng (CMN) với đường thẳng AB

Gọi E là giao điểm của MB và SB

Ta có \(E \in MP\)suy ra\(E \in (CMN)\)

Suy ra E là giao điểm của mặt phẳng (CMN) với đường thẳng SB

b) Vì M và E cùng thuộc (CMN) và (SAB) nên ME  là giao tuyến của hai mặt phẳng (CMN) và (SAB)

Vì E và C cùng thuộc (CMN) và (SBC) nên EC là giao tuyến của hai mặt phẳng (CMN) và (SBC)

Hoạt động 9

Hình 25 là hình nhr của khối rubik tam giác (Pyramix). Quan sát Hình 25 và trả lời các câu hỏi:

a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?

b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?

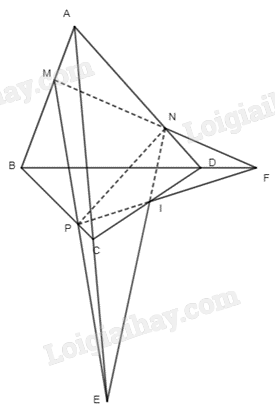
Phương pháp giải:

Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện

Lời giải chi tiết:

a) Khối rubik tam giác có 4 đỉnh. Các đỉnh không cùng nằm trong một mặt phẳng

b) Khối rubik tam giác có 4 mặt. Mỗi mặt của khối rucik tam giác là những hình tam giác.

Luyện tập 6

Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho:

\(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\)

a) Xác định E. F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP)

b) Chứng minh rằng các đường thẳng NE, PE và CD cùng đi qua một điểm

Phương pháp giải:

Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P), ta tìm giao điểm của a và một đường thẳng b nằm trong (P):

\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)

Bước 1: Xác định mp (Q) chứa a

Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)

Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)

Lời giải chi tiết:

a) Tam giác ABC có: MP cắt AC tại E

Mà MP thuộc (MNP)

Nên E là giao điểm của AC và (MNP)

Tam giác ABD có: MN cắt BD tại F

Mà MN thuộc (MNP)

Nên F là giao điểm của BD và (MNP)

b) Ta có: P thuộc BC

          F thuộc BD

Suy ra PF thuộc (BCD)

Do đó PF và CD cùng thuộc (BCD)

Nên PF và CD cắt nhau tại một điểm (1)

Ta có: N thuộc AD

          E thuộc AC

Suy ra NE thuộc (ACD)

Do đó NE và CD cắt nhau tại một điểm (2)

Từ (1) và (2) suy ra: NE, PE, CD cùng đi qua một điểm