Giải mục 4 trang 60, 61, 62, 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

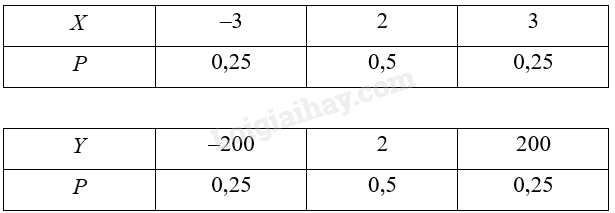
Hoạt động 4

Trả lời câu hỏi Hoạt động 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Cho hai biến ngẫu nhiên rời rạc \(X\) và \(Y\) có bảng phân bố xác suất như sau:

a) Hãy so sánh kì vọng của X và kì vọng của Y.

b) Biến ngẫu nhiên rời rạc nào có các giá trị “phân tán” rộng hơn?

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Lời giải chi tiết:

a) Kì vọng của \(X\) là: \(E\left( X \right) =  - 3.0,25 + 2.0,5 + 3.0,25 = 1\).

Kì vọng của \(Y\) là: \(E\left( Y \right) =  - 200.0,25 + 2.0,5 + 200.0,25 = 1\).

b) Y có độ phân tán rộng hơn.

Luyện tập 5

Trả lời câu hỏi Luyện tập 5 trang 61 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Hãy tính \(V\left( Y \right)\) ở Ví dụ 8 bằng công thức (1).

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).

Lời giải chi tiết:

Kì vọng của \(Y\) là: \(E\left( Y \right) =  - 200.0,25 + 2.0,5 + 200.0,25 = 1\).

Phương sai của \(X\) là: \(V\left( X \right) = {\left( { - 200} \right)^2}.0,25 + {2^2}.0,5 + {200^2}.0,25 - {1^2} = 20001\).

Luyện tập 6

Trả lời câu hỏi Luyện tập 6 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Mỗi ngày trong tuần, bác Linh sẽ chọn một trong ba phương tiện là xe đạp, xe máy hoặc xe buýt để đi đến cơ quan. Thời gian đi từ nhà đến cơ quan khi đi bằng xe đạp, xe máy hoặc xe buýt lần lượt là 20 phút, 10 phút và 12 phút. Biết rằng xác suất bác Linh chọn xe đạp, xe máy và xe buýt lần lượt là 0,3; 0,5 và 0,2. Chọn ngẫu nhiên một ngày trong tuần và gọi \(X\) là thời gian bác Linh đi từ nhà đến cơ quan ngày hôm đó. Tính kì vọng và phương sai của \(X\).

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).

Lời giải chi tiết:

Bảng phân bố xác suất của \(X\):

Kì vọng của \(X\) là: \(E\left( X \right) = 10.0,5 + 12.0,2 + 20.0,3 = 13,4\).

Phương sai của \(X\) là: \(V\left( X \right) = {10^2}.0,5 + {12^2}.0,2 + {20^2}.0,3 - {13,4^2} = 19,24\).

Vận dụng 2

Trả lời câu hỏi Vận dụng 2 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Hai xạ thủ Vinh và Huy cùng tập bắn vào một bia. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Vinh lần lượt là 0,4 và 0,3. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Huy lần lượt là 0,6 và 0,2. Điểm số xạ thủ đạt được khi bắn trúng vòng 10 và 9 lần lượt là 2 và 1. Nếu xạ thủ không bắn trúng hai vòng trên thì được 0 điểm.

a) Nếu so sánh theo kì vọng thì xạ thủ nào có kết quả bắn tốt hơn?

b) Nếu so sánh theo phương sai thì xạ thủ nào có kết quả bắn ổn định hơn?

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).

Lời giải chi tiết:

Gọi \(X\) và \(Y\) lần lượt là điểm của xạ thủ Vinh và xạ thủ Huy.

Xác suất để xạ thủ Vinh được 0 điểm là: \(1 - 0,4 - 0,3 = 0,3\).

Xác suất để xạ thủ Huy được 0 điểm là: \(1 - 0,6 - 0,2 = 0,2\).

Bảng phân bố xác suất của \(X\):

Bảng phân bố xác suất của \(Y\):

a) Kì vọng của \(X\) là: \(E\left( X \right) = 0.0,3 + 1.0,4 + 2.0,3 = 1\).

Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.0,2 + 1.0,6 + 2.0,2 = 1\).

Vậy nếu so sánh theo kì vọng thì hai xạ thủ có kết quả bắn tốt như nhau.

b) Phương sai của \(X\) là: \(V\left( X \right) = {0^2}.0,3 + {1^2}.0,4 + {2^2}.0,3 - {1^2} = 0,6\).

Phương sai của \(Y\) là: \(V\left( Y \right) = {0^2}.0,2 + {1^2}.0,6 + {2^2}.0,2 - {1^2} = 0,4\).

Vậy nếu so sánh theo phương sai thì xạ thủ Huy có kết quả bắn ổn định hơn.