Giải mục 3 trang 58, 59, 60 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Hoạt động 3

Trả lời câu hỏi Hoạt động 1 trang 58 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Khảo sát 40 học sinh lớp 12A về số xe máy có ở gia đình mỗi bạn. Kết quả được ghi vào bảng tần số sau:

Hỏi trung bình trong mỗi gia đình các bạn lớp 12A có bao nhiêu xe máy?

Phương pháp giải:

Sử dụng công thức tính số trung bình: \(\overline x  = \frac{{{m_1}.{x_1} + {m_2}.{x_2} + ... + {m_k}.{x_k}}}{n}\).

Lời giải chi tiết:

Trung bình trong mỗi gia đình các bạn lớp 12A có:

\(\overline x  = \frac{{4.0 + 12.1 + 18.2 + 6.3}}{{40}} = 1,65\) (xe máy).

Luyện tập 4

Trả lời câu hỏi Luyện tập 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Một hộp chứa 3 tấm thẻ cùng loại được đánh số từ 1 đến 3.

a) Lấy ra ngẫu nhiên 1 thẻ từ hộp. Gọi X là số ghi trên thẻ đó. Hãy tính kì vọng của X.

b) Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp. Gọi Y là số lớn hơn trong hai số ghi trên hai thẻ đó. Hãy tính kì vọng của Y.

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Lời giải chi tiết:

a) \(X\) nhận các giá trị là 1; 2; 3.

Xác suất để nhận được 3 tấm thẻ là như nhau và bằng: \(\frac{1}{3}\).

Bảng phân bố xác suất của \(X\):

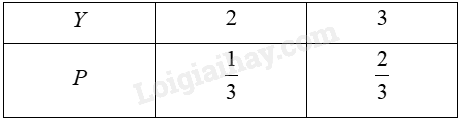
Kì vọng của \(X\) là: \(E\left( X \right) = 1.\frac{1}{3} + 2.\frac{1}{3} + 3.\frac{1}{3} = 2\).

b) \(Y\) nhận các giá trị là 2; 3.

TH1: Lấy ra thẻ 1 và 2. Khi đó: \(Y = 2\).

TH2: Lấy ra thẻ 1 và 3. Khi đó: \(Y = 3\).

TH3: Lấy ra thẻ 2 và 3. Khi đó: \(Y = 3\).

Vậy \(P\left( {Y = 2} \right) = \frac{1}{3},P\left( {Y = 3} \right) = \frac{2}{3}\).

Bảng phân bố xác suất của \(Y\):

Kì vọng của \(Y\) là: \(E\left( Y \right) = 2.\frac{1}{3} + 3.\frac{2}{3} = \frac{8}{3}\).

Vận dụng 1

Trả lời câu hỏi Vận dụng 1 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Ở một hội chợ, người ta tổ chức trò chơi có thưởng như sau: Có 3 quả bóng giống nhau được đánh số từ 1 đến 3 và 3 cái hộp giống nhau cũng được đánh số từ 1 đến 3. Người chơi bị bịt mắt và phải cho bóng vào hộp sao cho mỗi hộp có đúng 1 quả bóng. Ứng với mỗi quả bóng cho vào hộp có cùng số với nó, người chơi sẽ được thưởng 2000 đồng. Trước mỗi lượt chơi, người chơi phải mua vé ở chỗ quản trò với giá 1.000 đồng. Nếu so sánh về mặt trung bình thì người chơi hay quản trò có lợi hơn?

Phương pháp giải:

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

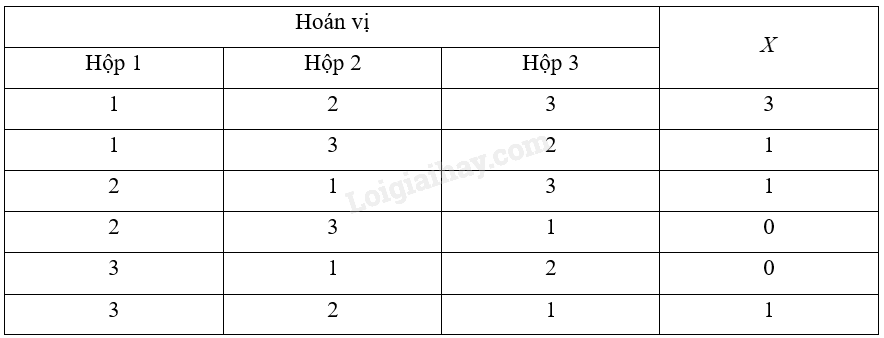
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Lời giải chi tiết:

Gọi \(X\) là số bóng được đặt vào hộp có cùng số với nó, \(Y\) là số tiền người chơi thu được.

Ta có:

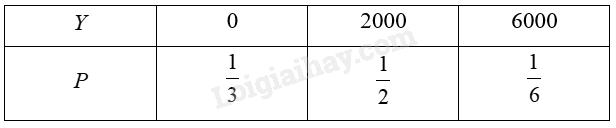
\(X\) nhận các giá trị là 0; 1; 3.

\(Y\) nhận các giá trị là 0; 2000; 6000.

Xác suất để \(Y\) nhận giá trị bằng 0 là: \(\frac{2}{6} = \frac{1}{3}\).

Xác suất để \(Y\) nhận giá trị bằng 2000 là: \(\frac{3}{6} = \frac{1}{2}\).

Xác suất để \(Y\) nhận giá trị bằng 6000 là: \(\frac{1}{6}\).

Bảng phân bố xác suất của \(Y\):

Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.\frac{1}{3} + 2000.\frac{1}{2} + 6000.\frac{1}{6} = 2000\).

Vậy số tiền thưởng trung bình trong mỗi lần chơi là 2000 đồng. Chi phí một lần chơi là 1000 đồng. Vậy xét theo trung bình thì người chơi có lợi hơn.