Giải mục 3 trang 18, 19, 20, 21 SGK Toán 8 – Chân trời sáng tạoHùng mua (x) mét dây điện và phải trả số tiền là (y) nghìn đồng. Giá trị tương ứng giữa (x)và (y) được cho bởi bảng sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
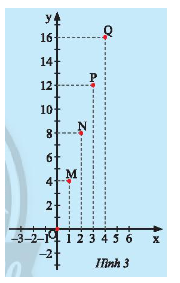
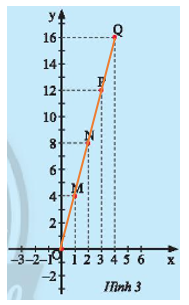
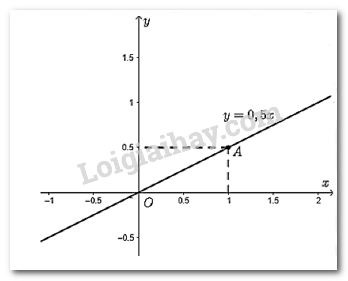
HĐ3 Video hướng dẫn giải Hùng mua \(x\) mét dây điện và phải trả số tiền là \(y\) nghìn đồng. Giá trị tương ứng giữa \(x\)và \(y\) được cho bởi bảng sau: Hùng vẽ các điểm \(M\left( {1;4} \right);N\left( {2;8} \right);P\left( {3;12} \right);Q\left( {4;16} \right)\) trên mặt phẳng tọa độ \(Oxy\) như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm \(O;M;N;P;Q\) có thẳng hàng không. Phương pháp giải: Dùng thước thẳng đặt vào các điểm để kiểm tra. Lời giải chi tiết: Dùng thước thẳng kiểm tra ta thấy các điểm \(O;M;N;P;Q\) thẳng hàng. TH3 Video hướng dẫn giải a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\). b) Các đồ thị sau đây là đồ thị của hàm số nào? Phương pháp giải: Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau: Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\). Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Để xác định một hàm số \(y = ax\) qua đồ thị ta lấy một điểm thuộc đồ thị và đi tìm ngược lại hệ số \(a\). Lời giải chi tiết: a) - Vẽ đồ thị hàm số \(y = 0,5x\) Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\) Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\). - Vẽ đồ thị hàm số \(y = - 3x\) Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\) Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
- Vẽ đồ thị hàm số \(y = x\) Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\) Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\). b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\). - Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\). Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\). - Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\). Do đó, đồ thị b là đồ thị của hàm số \(y = - x\). - Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\). Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\). HĐ4 Video hướng dẫn giải Cho hàm số \(y = f\left( x \right) = x\) và \(y = g\left( x \right) = x + 3\) a) Thay dấu ? bằng số thích hợp. b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị của hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) có trong bảng trên. c) Kiểm tra xem các điểm thuộc đồ thị hàm số của \(y = g\left( x \right)\) vẽ ở câu b có thẳng hàng không. Và dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\). Phương pháp giải: - Giá trị của hàm số \(y = f\left( x \right)\) tại điểm \(x = a\) là \(f\left( a \right)\). - Vẽ đồ thị hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) ta làm như sau: Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right)\). Bước 2: Biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\). - Dùng thước thẳng kiểm tra các điểm thẳng hàng. Lời giải chi tiết: a) - Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\); - Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\); - Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\); - Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\); - Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\); Ta có bảng sau:
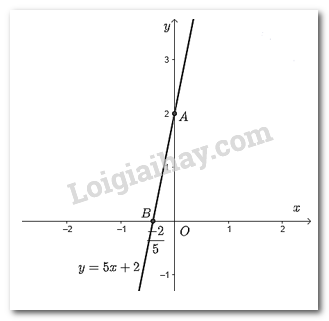
b) - Vẽ đồ thị hàm số \(y = f\left( x \right) = x\) Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\) Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\). - Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\). c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau. Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\): Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\). Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\). Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\). TH4 Video hướng dẫn giải Vẽ đồ thị của các hàm số sau: a) \(y = 5x + 2\); b) \(y = - 2x - 6\); Phương pháp giải: Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau: Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\). Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\). Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\). Lời giải chi tiết: a) \(y = 5x + 2\); Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\). Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{5}\) ta được điểm \(B\left( {\dfrac{{ - 2}}{5};0} \right)\) trên \(Ox\). Vẽ đường thẳng đi qua hai điểm \(A;B\) ta được đồ thị của hàm số \(y = 5x + 2\).
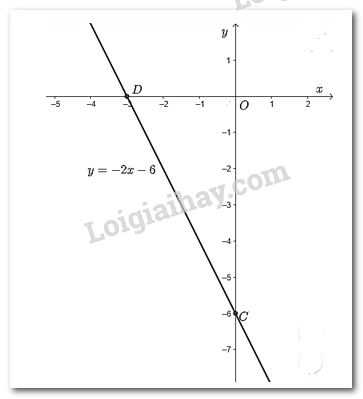
b) \(y = - 2x - 6\) Cho \(x = 0 \Rightarrow y = - 6\) ta được điểm \(C\left( {0; - 6} \right)\) trên trục \(Oy\). Cho \(y = 0 \Rightarrow x = - 3\) ta được điểm \(D\left( { - 3;0} \right)\) trên \(Ox\). Vẽ đường thẳng đi qua hai điểm \(C;D\) ta được đồ thị của hàm số \(y = - 2x - 6\).
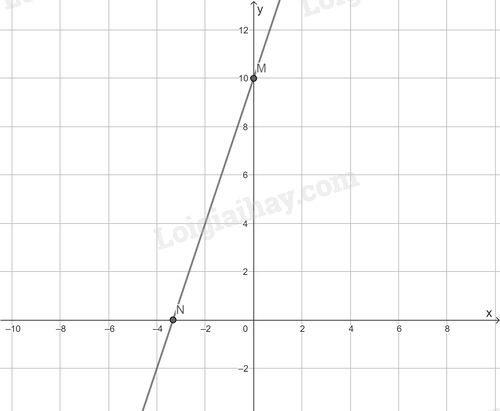
VD3 Video hướng dẫn giải Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm. a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật. b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\). Phương pháp giải: Độ dài của lò xo sau khi treo vật nặng bằng độ dài ban đầu của lò xo cộng với độ dài tăng thêm do bị ảnh hưởng của vật nặng. Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau: Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\). Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\). Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\). Lời giải chi tiết: Vì cứ treo thêm 1 kg vật nặng thì lò xo dài thêm 3 cm nên treo thêm \(x\) kg vật nặng thì lò xo dài thêm \(3x\) cm. Chiều dài của lò xo sau khi treo vật nặng là: \(y = 3x + 10\). b) Vẽ đồ thị hàm số \(y = 3x + 10\) Cho \(x = 0 \Rightarrow y = 10\) ta được điểm \(M\left( {0;10} \right)\) trên trục \(Oy\). Cho \(y = 0 \Rightarrow x = \dfrac{{ - 10}}{3}\) ta được điểm \(N\left( {\dfrac{{ - 10}}{3};0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = 3x + 10\) là đường thẳng đi qua hai điểm \(M;N\).
|


























Danh sách bình luận