Giải mục 3 trang 139 SGK Toán 11 tập 1 - Cùng khám pháBảng 5.12 cho biết về phân phối khối lượng của một nhóm 32 học sinh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 3 Bảng 5.12 cho biết về phân phối khối lượng của một nhóm 32 học sinh
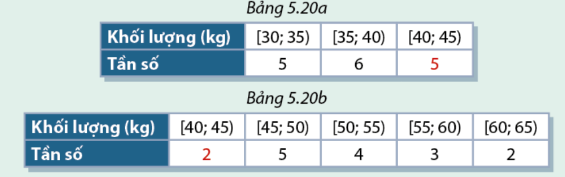
a, Xác định nhóm chứa trung vị \({M_e}\) của mẫu số liệu đã cho. Tính \({M_e}\) b, Kí hiệu \({u_1},{u_2},...{u_{32}}\) là các giá trị của mẫu số liệu được sắp xếp theo thứ tự không giảm. Nhóm dưới \({M_e}\) có bao nhiêu giá trị? Nhóm trên \({M_e}\) có bao nhiêu giá trị? c, Hãy giải thích vì sao Bảng 5.20 a và Bảng 5.20 b tương ứng là bảng phân bố tần số của nhóm dưới và bảng phân bố tần số của nhóm trên.
d, Tính các tứ phân vị thứ nhất \({Q_1}\) , (trung vị của nhóm dưới) và tứ phân vị thứ ba \({Q_3}\)( trung vị của nhóm trên) của mẫu số liệu cho trong Bảng 5.20 . Phương pháp giải: a, Lập bảng tần số ghép nhóm để xác định nhóm trung vị và công thức tính \({M_e}\) b, Dựa vào câu a để xác định c, Do khoảng cách nhóm trung vị là 5 và tần số nhóm là 7 nên chia đều khoảng cách có 5 giá trị nhỏ hơn \({M_e}\) và 2 giá trị lớn hơn bằng \({M_e}\). d, Dựa vào công thức tính trung vị để xác định \({Q_1}\), \({Q_3}\). Lời giải chi tiết: a,
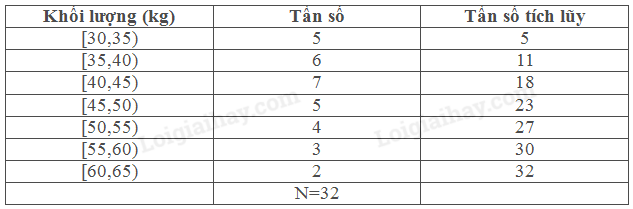
Ta có: \(\frac{N}{2} = \frac{{32}}{2} = 16\). Nhóm trung vị là [40,45). \({L_m} = 40\), \(\frac{N}{2} = \frac{{32}}{2} = 16\), T= 11,\({n_m} = 7\) , h= 5 \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 40 + \frac{{16 - 11}}{7}.5 \approx 43,57\) b, Do \({M_e}\) thuộc nhóm [40,45) nên Tổng giá trị nhỏ hơn \({M_e}\) là : 5+6=11 Tổng giá trị lớn hơn \({M_e}\) là: 2+5+4+3=14 c, Dựa vào câu c nên Bảng 5.20 a và Bảng 5.20 b tương ứng là bảng phân bố tần số của nhóm dưới và bảng phân bố tần số của nhóm trên. d Tính \({Q_1}\): Bảng tần số tích lũy
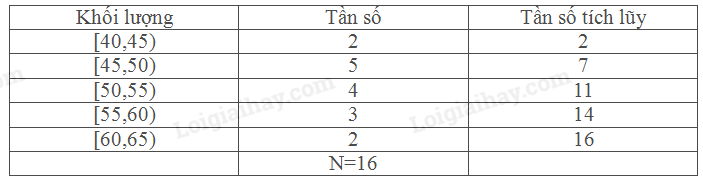
Ta có:\(\frac{N}{2} = \frac{{16}}{2} = 8\). Nhóm trung vị là [35,40). \({L_1} = 35\), \(\frac{N}{2} = \frac{{16}}{2} = 8\), T= 5,\({n_1} = 6\) , h= 5 \({Q_1} = {M_e} = {L_1} + \frac{{\frac{N}{2} - T}}{{{n_1}}}.h = 35 + \frac{{8 - 5}}{6}.5 = 37,5\) Tính \({Q_3}\): Bảng tần số tích lũy
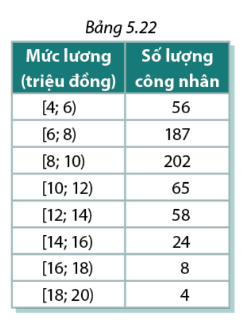
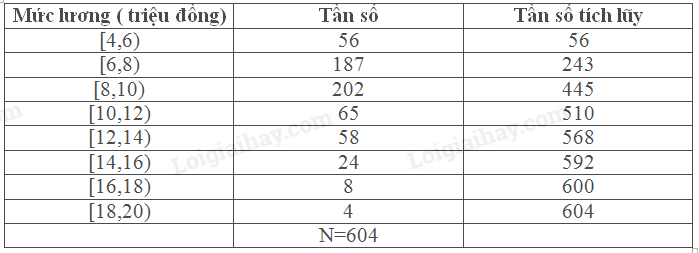
Ta có:\(\frac{N}{2} = \frac{{16}}{2} = 8\). Nhóm trung vị là [50,55). \({L_3} = 50\), \(\frac{N}{2} = \frac{{16}}{2} = 8\), T= 7,\({n_3} = 4\) , h= 5 \({Q_3} = {M_e} = {L_3} + \frac{{\frac{N}{2} - T}}{{{n_3}}}.h = 50 + \frac{{8 - 7}}{4}.5 = 51,25\) Luyện tập 3 Bảng 5.22 biểu diễn kết quả điều tra do Ban chấp hành Công đoàn của một xí nghiệp may thực hiện về lương hàng tháng của 604 công nhân và cán bộ lãnh đạo a, Ban chấp hành Công đoàn muốn đề nghị trợ cấp cho nhóm 25% số công nhân có mức lương thấp nhất trong công ty. Hãy ước tính mức lương cao nhất của nhóm công nhân này. ( làm tròn kết quả đến hai chữ số thập phân) b, Để có thêm thông tin nhằm hoạch định vấn đề lương thưởng cho năm tới, Ban giám đốc căn cứ vào 50% công nhân có lương nằm ở trung tâm của mẫu số liệu. Hãy xác định mức lương thấp nhất và mức lương cao nhất của nhóm công nhân này ( làm tròn kết quả đến hai chữ số thập phân)
Phương pháp giải: a, Tính \({Q_1}\) để tìm mức lương cao nhất của 25% số công nhân b, Tính \({Q_2}\) và \({Q_3}\) Lời giải chi tiết: a, Bảng tần số tích lũy
Ta có: \(\frac{N}{2} = \frac{{604}}{2} = 302 \Rightarrow \frac{N}{4} = \frac{{604}}{4} = 151 \Rightarrow \frac{{3N}}{4} = 453\) Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [6,8), [8,10) và [10,12) Độ dài các nhóm ghép đều bằng 2 Ta có: \({L_1} = 6,{n_1} = 187,{T_1} = 56\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 6 + \frac{{151 - 56}}{{187}}.2 \approx 7,02\)( triệu đồng) Mức lương cao nhất của nhóm công ty này là xấp xỉ 7,02 triệu đồng b, Ta có: \({L_2} = 8,{n_2} = 202,{T_2} = 243\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 8 + \frac{{302 - 243}}{{202}}.2 \approx 8,58\) \({L_3} = 10,{n_3} = 65,{T_3} = 445\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 10 + \frac{{453 - 445}}{{65}}.2 \approx 10,25\) Vậy mức lương cao nhất và thấp nhất của 50% nhóm công nhân trung tâm là xấp xỉ 10,25 triệu đồng và 8,58 triệu đồng.
|






















Danh sách bình luận