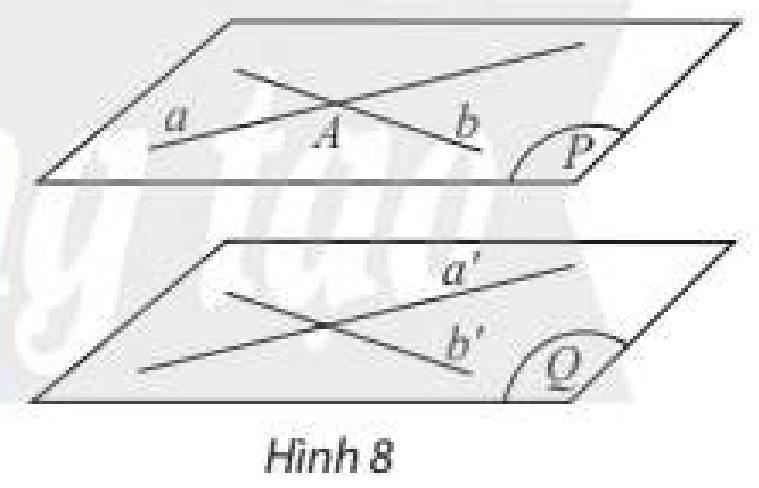
Giải mục 3 trang 109, 110, 111, 112, 113, 114, 115, 116 SGK Toán 11 tập 1 - Chân trời sáng tạoa) Cho điểm (A) ở ngoài mặt phẳng (left( Q right)). Trong (left( Q right)) vẽ hai đường thẳng cắt nhau (a') và (b'). Làm thế nào để vẽ hai đường thẳng (a) và (b) đi qua (A) và song song với (left( Q right))? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 115 SGK Toán 11 Chân trời sáng tạo a) Cho điểm \(A\) ở ngoài mặt phẳng \(\left( Q \right)\). Trong \(\left( Q \right)\) vẽ hai đường thẳng cắt nhau \(a'\) và \(b'\). Làm thế nào để vẽ hai đường thẳng \(a\) và \(b\) đi qua \(A\) và song song với \(\left( Q \right)\)? b) Có nhận xét gì về mối liên hệ giữa \(mp\left( {a,b} \right)\)và \(\left( Q \right)\)?
Phương pháp giải: Sử dụng các định lí: ‒ Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó. ‒ Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\). Lời giải chi tiết: a) Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(a\) song song với đường thẳng \(a'\). Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(b\) song song với đường thẳng \(b'\). Ta có: \(\begin{array}{l}\left. \begin{array}{l}a\parallel a'\\a' \subset \left( Q \right)\end{array} \right\} \Rightarrow a\parallel \left( Q \right)\\\left. \begin{array}{l}b\parallel b'\\b' \subset \left( Q \right)\end{array} \right\} \Rightarrow b\parallel \left( Q \right)\end{array}\) b) Ta có: \(\left. \begin{array}{l}a\parallel \left( Q \right)\\b\parallel \left( Q \right)\\a,b \subset mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right)\parallel \left( Q \right)\) HĐ4 Trả lời câu hỏi Hoạt động 4 trang 115 SGK Toán 11 Chân trời sáng tạo Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) thoả mãn \(\left( P \right)\parallel \left( Q \right)\), \(\left( R \right) \cap \left( P \right) = a\) và \(\left( R \right) \cap \left( Q \right) = b\). Xét vị trí tương đối của \(a\) và \(b\).
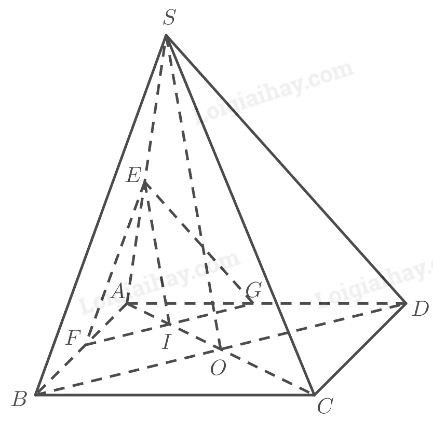
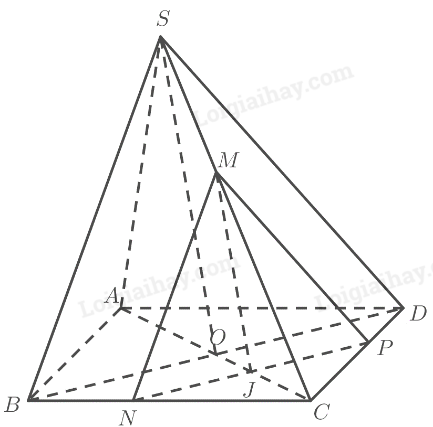
Phương pháp giải: Sử dụng định nghĩa: Hai đường thẳng gọi là song song nếu chúng nằm trong cùng một mặt phẳng và không có điểm chung. Lời giải chi tiết: Ta có: \(\left. \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\\left( P \right)\parallel \left( Q \right)\end{array} \right\} \Rightarrow a \cap b = \emptyset \). Vì hai đường thẳng \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( R \right)\) và không có điểm chung nên \(a\parallel b\). TH2 Trả lời câu hỏi Thực hành 2 trang 116 SGK Toán 11 Chân trời sáng tạo Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm của hai đường chéo, tam giác \(SBD\) là tam giác đều. Một mặt phẳng \(\left( \alpha \right)\) di động song song với mặt phẳng \(\left( {SBD} \right)\) và cắt đoạn thẳng \(AC\). Chứng minh các giao tuyến của \(\left( \alpha \right)\) với hình chóp tạo thành một tam giác đều. Phương pháp giải: ‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song. ‒ Sử dụng định lí Thales trong tam giác. Lời giải chi tiết:
TH1: \(\left( \alpha \right)\) cắt đoạn \(AO\) tại \(I\). Gọi \(E,F,G\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SA,AB,AD\). Ta có: \(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = FG\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow FG\parallel B{\rm{D}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{AG}}{{AD}} = \frac{{FG}}{{B{\rm{D}}}}\left( 1 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = EF\\\left( {SAB} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow EF\parallel SB \Rightarrow \frac{{AF}}{{AB}} = \frac{{AE}}{{AS}} = \frac{{EF}}{{SB}}\left( 2 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAD} \right) = EG\\\left( {SAD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow EG\parallel SD \Rightarrow \frac{{AG}}{{AD}} = \frac{{AE}}{{AS}} = \frac{{EG}}{{SD}}\left( 3 \right)\end{array}\) Từ (1), (2) và (3) suy ra \(\frac{{EF}}{{SB}} = \frac{{EG}}{{S{\rm{D}}}} = \frac{{FG}}{{B{\rm{D}}}}\). Tam giác \(SBD\) đều nên \(SB = SD = BD\). Do đó \(EF = EG = FG\). Vậy tam giác \(EFG\) đều. TH2: \(\left( \alpha \right)\) cắt đoạn \(CO\) tại \(J\). Gọi \(M,N,P\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SC,BC,C{\rm{D}}\).
Ta có: \(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = NP\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow NP\parallel B{\rm{D}} \Rightarrow \frac{{CN}}{{CB}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\left( 4 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SBC} \right) = MN\\\left( {SBC} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow MN\parallel SB \Rightarrow \frac{{CM}}{{C{\rm{S}}}} = \frac{{CN}}{{CB}} = \frac{{MN}}{{SB}}\left( 5 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SCD} \right) = MP\\\left( {SCD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow MP\parallel SD \Rightarrow \frac{{C{\rm{M}}}}{{C{\rm{S}}}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{MP}}{{SD}}\left( 6 \right)\end{array}\) Từ (4), (5) và (6) suy ra \(\frac{{MN}}{{SB}} = \frac{{MP}}{{S{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\). Tam giác \(SBD\) đều nên \(SB = SD = BD\). Do đó \(MN = MP = NP\). Vậy tam giác \(MNP\) đều. VD2 Trả lời câu hỏi Vận dụng 2 trang 116 SGK Toán 11 Chân trời sáng tạo Khi dùng dao cắt các lớp bánh (Hình 11), giả sử bề mặt của các lớp bánh là các mặt phẳng song song và con dao được xem như mặt phẳng \(\left( P \right)\), nêu kết luận về các giao tuyến tạo bởi \(\left( P \right)\) với các bề mặt của các lớp bánh. Giải thích.
Phương pháp giải: Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song. Lời giải chi tiết: Bởi vì các lớp bánh là các mặt phẳng song song với nhau nên theo định lí 3, giao tuyến tạo bởi \(\left( P \right)\) và các lớp bánh song song với nhau.
|






















Danh sách bình luận