Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều

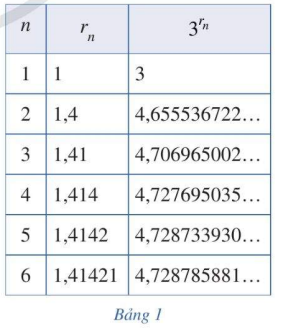
HĐ 5

Xét số vô tỉ: $\sqrt 2  = 1,4142135624...$. Xét dãy số hữu tỉ: ${r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...$ và $\lim {r_n} = \sqrt 2$. Bằng cách tính ${3^{{r_n}}}$ tương ứng, ta nhận được Bảng 1 ghi các dãy số $\left( {{r_n}} \right)$ và $\left( {{3^{{r_n}}}} \right)$ với n = 1, 2, …, 6. Người ta chứng minh được rằng khi $n \to  + \infty$ thì dãy số $\left( {{3^{{r_n}}}} \right)$ dần đến một giới hạn mà ta gọi là ${3^{\sqrt 2 }}$. Nêu dự đoán về giá trị của số ${3^{\sqrt 2 }}$ (đến hàng phần trăm).

Phương pháp giải:

Dựa vào giới hạn của dãy số hữu tỉ để dự đoán

Lời giải chi tiết:

Do ${r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...$ => ${3^{\sqrt 2 }} \approx 1,41$

Quảng cáo

LT 5

So sánh ${10^{\sqrt 2 }}\,\,và \,\,10$

Phương pháp giải:

Dựa vào dự đoán ở ví dụ 5 để so sánh

Lời giải chi tiết:

Do ${10^{\sqrt 2 }} \approx 25,95 > 10 \Rightarrow {10^{\sqrt 2 }} > 10$

HĐ 6

Nêu những tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương

Phương pháp giải:

Dựa vào các kiến thức đã học về lũy thừa ở cấp 2 để làm bài

Lời giải chi tiết:

+ ${a^\alpha }.{a^\beta } = {a^{\alpha  + \beta }}$

+ $\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha  - \beta }}$

+ ${\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }}$

+ ${(ab)^\alpha } = {a^\alpha }.{b^\alpha }$

+ ${\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}$

+ Nếu a > 1 thì ${a^\alpha } > {a^\beta } \Leftrightarrow \alpha  < \beta$

               + Nếu 0 < a < 1 thì ${a^\alpha } > {a^\beta } \Leftrightarrow \alpha  > \beta$

LT 6

Không sử dụng máy tính cầm tay, hãy so sánh các số: ${2^{2\sqrt 3 }}\,\,và \,\,{2^{3\sqrt 2 }}$

Phương pháp giải:

Dựa vào Ví dụ 7 để làm

Lời giải chi tiết:

Ta có:

$\left. \begin{array}{l}{\left( {2\sqrt 3 } \right)^2} = 12\\{\left( {3\sqrt 2 } \right)^2} = 18\end{array} \right\} \Rightarrow 2\sqrt 3  < 3\sqrt 2  \Rightarrow {2^{2\sqrt 3 }} < {2^{3\sqrt 2 }}$

LT 7

Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm):

a) $(-2,7)^{-4}$;

b) $\sqrt 3 - 1)^{\sqrt[3] {4} + 1}$

Phương pháp giải:

Sử dụng máy tính để tính, làm tròn đến hàng phần trăm.

Lời giải chi tiết:

a) $(-2,7)^{-4} \approx 0,02$;

b) $\sqrt 3 - 1)^{\sqrt[3] {4} + 1} \approx 0,45$