Giải mục 2 trang 24 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ2

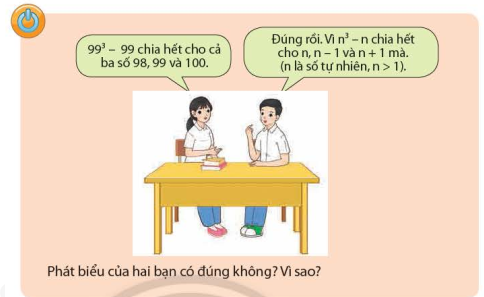
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:

a) \(4{x^2} - 9 \);

b) \({x^2}{y^2} - \dfrac{1}{4}{y^2}\)

Phương pháp giải:

Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)

Lời giải chi tiết:

a) \(4{x^2} - 9 = {\left( {2x} \right)^2} - {3^2} = \left( {2x + 3} \right)\left( {2x - 3} \right)\)

b) \({x^2}{y^2} - \dfrac{1}{4}{y^2} = {\left( {xy} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = \left( {xy + \dfrac{1}{2}y} \right)\left( {xy - \dfrac{1}{2}y} \right)\)\( = y\left( {x + \dfrac{1}{2}} \right)y\left( {x - \dfrac{1}{2}} \right) = {y^2}\left( {x + \dfrac{1}{2}} \right)\left( {x - \dfrac{1}{2}} \right)\)

Thực hành 2

Phân tích các đa thức sau thành nhân tử:

a) \(9{x^2} - 16\)                    b) \(4{x^2} - 12xy + 9{y^2}\)             c) \({t^3} - 8\) d) \(2a{x^3}{y^3} + 2a\)

Phương pháp giải:

a) Sử dụng hằng đăng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)

b) Sử dụng hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)

c) Sử dụng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)

d) Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\)

Lời giải chi tiết:

a) \(9{x^2} - 16\)\( = {\left( {3x} \right)^2} - {4^2} = \left( {3x + 4} \right)\left( {3x - 4} \right)\)

b) \(4{x^2} - 12xy + 9{y^2}\)\( = {\left( {2x} \right)^2} - 2.2x.3y + {\left( {3y} \right)^2} = {\left( {2x - 3y} \right)^2}\)

c) \({t^3} - 8\)\( = {t^3} - {2^3} = \left( {t - 2} \right)\left( {{t^2} + 2t + 4} \right)\)

d) \(2a{x^3}{y^3} + 2a\)\( = 2a\left( {{x^3}{y^3} + 1} \right) = 2a\left( {xy + 1} \right)\left( {{x^2}{y^2} - xy + 1} \right)\)

Vận dụng 1

Tìm một hình hộp chữ nhật có thể tích \(2{x^3} - 18x\) với (\(x > 3\)) mà độ dài các cạnh đều là biểu thức chứa \(x\).

Phương pháp giải:

Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.

Lời giải chi tiết:

Ta có:

\(2{x^3} - 18x = 2x\left( {{x^2} - 9} \right) = 2x\left( {x + 3} \right)\left( {x - 3} \right)\)

Vậy hình hộp có ba kích thước là \(2x\), \(x + 3\), \(x - 3\)

Vận dụng 2

Giải đáp câu hỏi mở đầu (trang 23)

Phương pháp giải:

Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.

Lời giải chi tiết:

Ta có:

\({99^3} - 99 = 99.({99^2} - 1) = 99.\left( {99 + 1} \right).\left( {99 - 1} \right) = 99.100.98\) chia hết cho \(98\), \(99\), \(100\)

\({n^3} - n = n\left( {{n^2} - 1} \right) = n\left( {n + 1} \right)\left( {n - 1} \right)\) chia hết cho \(n\), \(n - 1\), \(n + 1\) (\(n\) là số tự nhiên, \(n > 1\))