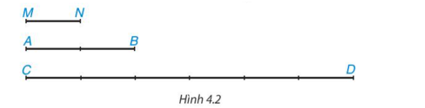
Giải mục 1 trang 77, 78 SGK Toán 8 tập 1 - Kết nối tri thứcCho Hình 4.2, em hãy thực hiện các hoạt động sau: Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số (dfrac{{AB}}{{C{rm{D}}}}) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
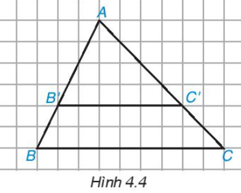
HĐ 1 Video hướng dẫn giải Cho Hình 4.2, em hãy thực hiện các hoạt động sau: Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\) Phương pháp giải: Quan sát hình 4.2 chọn MN = 1 (đvđd) khi đó tính được độ dài AB và CD và tình tỉnh số \(\dfrac{{AB}}{{C{\rm{D}}}}\) Lời giải chi tiết: Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd). Khi đó, AB = 2 (đvđd); CD = 6 (đvđd). Do đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{2}{6} = \dfrac{1}{3}\) Vậy AB = 2 (đvđd); CD = 6 (đvđd); \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{1}{3}\) HĐ 2 Video hướng dẫn giải Cho Hình 4.2, em hãy thực hiện các hoạt động sau: Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\) Phương pháp giải: Quan sát hình 4.2 và dùng thước thẳng để đo độ dài đoạn thẳng AB và CD Lời giải chi tiết: Đo độ dài các đoạn thẳng, ta được: AB = 4,8 cm; CD = 14,4 cm. Khi đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{{4,8}}{{14,4}} = \dfrac{1}{3}\) HĐ 3 Video hướng dẫn giải So sánh hai tỉ số tìm được trong hai hoạt động trên Phương pháp giải: Dựa vào tỉ số của hai hoạt động 1, 2. Lời giải chi tiết: Tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\) tìm được ở Hoạt động 1 và hoạt động 2 bằng nhau và đều bằng \(\dfrac{1}{3}\) Luyện tập 1 Video hướng dẫn giải Tính tỉ số của các đoạn thẳng có độ dài như sau: a) MN = 3 cm và PQ = 9 cm. b) EF = 25 cm và HK = 10 dm. Phương pháp giải: Dựa vào độ dài các đoạn thẳng đã cho ta tính tỉ số (đổi các đơn vị để cùng đơn vị đo) Lời giải chi tiết: a) Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{MN}}{{PQ}} = \dfrac{3}{9} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = \dfrac{9}{3} = 3\) Vậy: \(\dfrac{{MN}}{{PQ}} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = 3\) b) Đổi 10dm = 100cm Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{EF}}{{HK}} = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = \dfrac{{100}}{{25}} = 4\) Vậy: \(\dfrac{{EF}}{{HK}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = 4\) Luyện tập 2 Video hướng dẫn giải Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC, cắt A tại C’ (H.4.4 Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức: a) \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\) b) \(\dfrac{{AB'}}{{B'B}}\) và \(\dfrac{{AC'}}{{C'C}}\) c) \(\dfrac{{B'B}}{{AB}}\) và \(\dfrac{{C'C}}{{AC}}\) Phương pháp giải: Quan sát hình 4.4 Lời giải chi tiết: a) Từ hình vẽ ta thấy: \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{4}{6} = \dfrac{2}{3}\) Do đó, \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\) b) Từ hình vẽ, ta thấy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{4}{2} = \dfrac{2}{1};\dfrac{{AC'}}{{C'C}} = \dfrac{4}{2} = \dfrac{2}{1}\) Vậy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) c) Từ hình vẽ ta thấy: \(\dfrac{{B'B}}{{AB}} = \dfrac{2}{6} = \dfrac{1}{3};\dfrac{{C'C}}{{AC}} = \dfrac{2}{6} = \dfrac{1}{3}\) Do đó: \(\dfrac{{B'B}}{{AB}} = \dfrac{{C'C}}{{AC}}\)
|




















Danh sách bình luận