Giải mục 1 trang 73, 74 SGK Toán 8 tập 2– Chân trời sáng tạoa) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
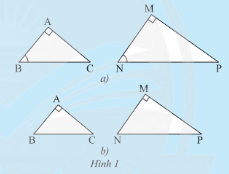
HĐ1 Video hướng dẫn giải a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\widehat B = \widehat N\) thì hai tam giác đó có đồng dạng với nhau không. b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) thì hai tam giác đó có đồng dạng với nhau không. Phương pháp giải: - Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau. - Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng. Lời giải chi tiết: a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có: \(\widehat B = \widehat N\) (giả thuyết) \(\widehat A = \widehat M = 90^\circ \). Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g) b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có: \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết) \(\widehat A = \widehat M = 90^\circ \). Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c). TH1 Video hướng dẫn giải Cho tam giác \(DEF\) vuông tại \(D\) có \(DH\) là đường cao (Hình 3). Chứng minh rằng \(D{E^2} = EH.EF\)
Phương pháp giải: Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau. Lời giải chi tiết: Vì \(DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ \) Xét tam giác \(DEH\) và tam giác \(FED\) ta có: \(\widehat E\) chung \(\widehat {DHE} = \widehat {EDF} = 90^\circ \). Do đó, \(\Delta DEH\backsim\Delta FED\) (g.g) Suy ra, \(\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH\) (điều phải chứng minh). VD1 Video hướng dẫn giải Tính chiều cao của cột cờ trong hoạt động khởi động trang 73. Phương pháp giải: Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau. Lời giải chi tiết:
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\). Xét tam giác \(DEF\) và tam giác \(ABC\) ta có: \(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên) \(\widehat {EDF} = \widehat {BAC} = 90^\circ \). Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g) Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\). Vậy cột cờ \(AB\) cao 8m.
|






















Danh sách bình luận